Una guía compacta a la compactificación...

En su momento escribí una entrada sobre la forma más básica de compactificación, la teoría de Kaluz-Klein. Si se quieren más detalles (en especial cómo aparece, y que papel juega el dilatón) de los que vienen en esa entrada se puede consultar, por ejemplo, la correspondiente entrada de la wikipedia inglesa Kaluza–Klein theory.

Bien, voy a intentar avanzar un poco más respecto a lo que ahí viene y dar una idea un poco global de cómo es el proceso de compactificación. Al intentar dar una idea global dejaré de lado bastantes detalles técnicos, pero tampoco va a ser a nivel de un libro de divulgación para legos sino más bien en la línea de la entrada anterior.

El siguiente paso, una vez tenemos una teoría guague abeliana U(1), es intentar obtener una teoría no abeliana, para lo cual vamos a necesitar mas de una dimensión adicional, usando la notación de la entrada anterior descomponemos la métrica en la forma:

Recordemos que M y N son índices que recorren todas las dimensiones, mu y nu recorren sólo las 4 dimensiones usuales, eta es la métrica de Minkowsky e y denota las coordenadas en las dimensiones extra.

Asumimos que esta métrica es una solución a las ecuaciones de Einstein para el vacío  o bien, sí permitimos una constante cosmológica

En el caso de una sóla dimensión adicional la compactificación era única, convertir el eje y en un círculo, ahora tenemos mucha más libertad. 

Sí tenemos D dimensiones extra y plegamos cada uno de los ejes coordenados en un círculo tendremos un D-toro (recordemos que el 2-toro tiene forma de “donut” hueco, o de neumático) y, en ése caso, la gravedad de las dimensiones extra se verá cómo una teoría gauge . Más adelante explicaré cómo se obtiene ese D-toro, pero de momento entendamos bien lo que hemos hecho. Cuando las dimensiones extra están descompactificadas ahí opera la simetría del grupo de difeormorfismos de esas dimensiones extra, que es muy grande.

 Al reducir esas dimensiones a la forma de un D-toro esa simetría de difeomorfismos se ha visto muy reducida, a ese . Digamos que el grupo de isommetrías de la dimensión compactificada se ve cómo una teoría gauge con esa misma simetría en las 4 dimensiones.

Cuando las dimensiones extra se compactifican a una geometría más compleja que un D-toro y no es nada sencillo ver las isometrías de ese espacio. Voy a entrar un poco en algunos detalles matemáticos, elementales, pero que no siempre se comentan en los libros de física sobre el proceso de compactificación (sobre los detalles de las isomerías hablaré en otra entrada). Lo primero es el origen del término “compactificar”. Hace referencia al concepto topológico de espacio compacto. 

Lo escribí en la entrada que dediqué a un libro sobre la conjetura de Poincaré pero lo reescribiré aquí, para hacer ésto más autocontenido.

Las nociones de continuidad en cálculo se suelen dar en términos de epsilones y deltas, pero eso en esencia es hablar de entornos abiertos de la recta real, y el caso es que si uno lo analiza uno usa sólo 3 propiedades básicas de los abiertos.

Una topología es recoger esas tres propiedades y convertirlas en axiomas.

Sea X un conjunto y sea Y={Xn} una colección finita o infinita de subconjuntos de X, X e Y forman un espacio topológico si

i. el conjunto vacío e Y pertenecen a Y

ii. Cualquier subcolección finita o infinita {Zn} de Xn tiene la propiedad de que la unión de todos los Zn pertenece a Y

iii. Cualquier subcolección finita {Zm} de los Xn tiene la propiedad de que su intersección pertenece a Y.

Los Xn son los abiertos de esa topología. Conviene hacer una pequeña distinción, que no siempre se explica en los libros de topología/geometría para físicos. Los intervalos epsilón y deltas del cálculo de una varible, y sus generalizaciones elementales, los discos abiertos de radio epsilon/delta en el plano, las bolas abiertas en tres dimensiones, etc, son un tipo especial de abiertos, pero, ciertamente, hay conjuntos que son abiertos y no son de esa forma. Esos subconjuntos especiales de la topología forman una base de la misma.

Bien, una vez que tenemos definidos los abiertos cualquier definición que hagamos en términos de esos conjuntos va a ser una definición topológica.

 Por ejemplo se dice que un conjunto es cerrado cuando su complementario es abierto. Otra noción topológica de interés es la de compacidad. Intuitivamente en  un compacto va a ser un conjunto cerrado y acotado (la distancia entre dos cualesquiera de sus puntos es finita).

Pero como dije una noción topológica debe darse en términos de los abiertos.

 Vamos a ello.

Primero debo explicar la idea de recubrimiento. Dado un subconjunto, S, de un espacio topológico, X un recubrimiento de S es una colección de conjuntos abiertos Rn tal que S está incluido en la unión de todos los Rn. Se dirá que un conjunto es compacto cuando todo recubrimiento del mismo admite un subrecubrimiento (un cubrimiento con un un subconjunto de la colección recubridora)finito. La noción de compacidad es útil por muy diversos motivos. Una es que, por el teorema de Heine-Borel, podemos caracterizar los cerrados y acotados, un tipo de conjuntos interesante, mediante 

esta propiedad.

Otro aspecto útil es que si queremos demostrar algo sobre un compacto nos basta demostrarlo sobre cualquier elemento del conjunto recubridor y asegurarnos de que la propiedad demostrada no se pierde cuando tenemos una unión finita de esos elementos. Es importante hacer notar que como en un compacto todos los recubrimientos admiten subrecubrimiento finito podemos elegir los Rn de la forma que más nos convenga.

Tan importante es la noción de compacidad que la mayoría de resultados topológicos van a estar referidos a espacios compactos.

 Los no compactos son mucho más difíciles de estudiar.

Entonces la idea de la compactificación es coger un conjunto que no es compacto, por ejemplo la recta real, que no es acotada, y por tanto, según el teorema de Heine-Borel no es compacta, y convertirla en un conjunto compacto por un procedimiento bien definido, en este caso identificar los dos puntos del infinito a la “izquierda” y “derecha”. 

Si tomamos un folio e identificamos dos lados opuestos obtenemos la superficie de un cilindro (sin las tapas). Sí en ese cilindro resultante identificamos los dos círculos opuestos obtenemos un 2-toro.

ES interesante que, en el caso anterior, tanto el folio (un rectángulo con sus lados incluidos) como el toro son compactos así que aquí no estaría del todo justificado el término “compactificación”. Pero sí nos imaginamos que el rectángulo es infinito, es decir, es el plano real, entonces sí estamos convirtiendo ese plano, que no es compacto, en un toro, que es compacto. Realmente el proceso de compactificación de un rectángulo aunque no cambia la compacidad del rectángulo si cambia otras propiedades topológicas del mismo, por ejemplo la conectividad por arcos (la explico en la entrada sobre la conjetura de Poincaré). 

El rectángulo es contractible (cualquier círculo que dibuje dentro del mismo se puede contraer a un punto sin salirse del rectángulo) mientras que en el toro no es así (de hecho hay dos familias de círculos que no pueden contraerse a un punto). No daré más detalles sobre ésto ahora (en el post sobre la conjetura de Poincaré comento más al respecto) pero no deja de ser un hecho interesante, que tiene muchas implicaciones en topología y en física.

Uno, bastante conocido, es que, en teoría de cuerdas, en particular para la cuerda heterótica compactificada en un Calabi-Yau, el número de generaciones de partículas es igual a la mitad de la característica de Euler-Poincaré de el espacio de compactificación 

Esta constante apareció por primera vez en el trabajo sobre teoría grafos que hizo Euler para, entre otras cosas, resolver el problema de los puentes de Königsberg. Para un grafo la expresión de la característica de Euler es 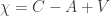 donde C, A y V son los números de caras, de aristas y de vértices respectivamente.

Cómo una superficie puede ser triangulada se puede definir esa constante en términos de la constante de Euler de la triangulación de la misma. No obstante, para una superficie, o una variedad n-dimensional, es mejor definir la constante en términos de los grupos de homología o cohomología. 

Primero se define el n-ésimo número de Betti  como el rango del n-ésimo grupo de homología. En términos de esos números la característica de ÇEuler es la suma alternada de los números de Betti, es decir, tiene la expresión 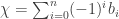. También, mediante la dualidad de Poincaré, se podría escribir en términos de grupos de cohomología, así cómo en otras formas más sofisticadas, pero éso ya sería irnos demasiado del propósito de la entrada.

Otro ejemplo es el uso de “Wilson loops” (o Wilson lines), osea, holonomías sobre círculos, que cuando el espacio no es conexo por arcos pueden usarse para reducir la simetría de un grupo gauge de una manera diferente al mecanismo de Higgs. Este procedimiento se usa de manera habitual en la fenomenología de la cuerda heterótica.

Por cierto, el plano real puede ser compactificado de manera natural de más de una forma. Un proceso muy típico sería la compactificación por un punto, el punto del infinito, es decir, cogemos todos las regiones del plano que “están en el infinito” y las convertimos en un punto. 

El espacio resultante sería una esfera. Es un proceso algo más complejo de visualizar, y para ayudar a entenderlo vendría bien que explicase la proyección estereográfica, pero espero que con esta imagen os hagáis una idea aproximada.

Al inicio de la entrada mencioné que iba a explicar cómo surgía el D-toro al compactificar cada una de las dimensiones extra a un círculo. Hasta ahora he explicado cómo obtener el toro identificando los lados opuestos de un cuadrado, pero ahí no se ve cómo surge a partir de círculos.

Bien, éso requiere el concepto de producto cartesiano de dos espacios topológicos. Sí tenemos dos espacios topológicos X1 y X2 su producto cartesiano es el conjunto X1xX2={x1,x2}, es decir, el conjunto de pares donde el primer par, x1, es un elemento del conjunto X1 y el segundo, x2, es un elemento del conjunto X”. 

A partir de una base de las topología de X1 y X2 se puede formar una base de la topología producto tomando el conjunto de todos los pares ordenados posibles formados con los elementos base. En caso de que no se haya entendido muy bien este párrafo tampoco pasa nada, que es bastante fácil de visualizar la explicación que daré ahora.

Si tenemos dos círculos  y , el toro es el producto cartesiano de esos dos círculos . Intuitivamente podemos pensar que cogemos uno de los círculos y cada uno de los puntos de ese círculo lo hacemos girar 360 grados alrededor de otro círculo perpendicular. 

Se puede visualizar en el siguiente dibujo bastante bien la idea.

Obviamente un D-toro es la generalización de esa idea, osea, un producto cartesiano de D círculos, cada uno de los cuales se obtiene al compactificar cada uno de los ejes coordenados.