Cuántos primos hay...?

¿Cuántos?

 Es posible que muchos de los lectores de estos blogs conozcan la respuesta

 y esperen artículos algo más avanzados, pero creo que esta demostración 

es una de las joyas de las matemáticas, y por su simplicidad es accesible

 a todo el que tenga interés en conocerla.

 A mí me cautivó en su momento.

Y lo sigue haciendo cuando piensen en ella.

Una vez leí que una buena demostración debe ser obvia, clara 

y elegante. 

 La demostración es clara.

Y una vez entendida, el asunto parece obvio y la elegancia es innegable.

Bien, al asunto pues. 

¿Cuántos números primos hay?

 Quizá sería buena idea refrescar la memoria:

un número primo es aquel que es divisible solamente por sí mimo y la unidad. 

Así, 5 es un número primo, pues es solamente divisible por sí mismo 

y la unidad.4 NO es primo, porque aparte de por sí mismo y la unidad, 

también es divisible por 2.

Una vez definido los números primos, queda la cuestión de su cantidad.

 ¿Son infinitos o finitos, y en este caso, cuántos son? 

 Bueno, la respuesta nos fue dada por Euclides, en una de las mejores demostraciones de las matemáticas, como ya he dicho,

 y la resupesta es que los números primos son infinitos.

Sin más preámbulo, allá va:

Primero, vamos a suponer que los números primos son finitos.

Esto es, suponemos que hay un número determinado de primos, y a partir

 del último no encontramos ninguno más.

Entonces, partiendo de esta premisa, y siguiendo unos pasos lógicos, 

vamos a llegar a una contradicción, a un absurdo.

Como asumir la veracidad de la premisa nos lelva a un absurdo,

 debemos concluir que la premisa es falsa, y su contraria, (que los números primos son infinitos) es verdadera.

Vamos a ello:

Supongamos que los números primos son finitos, supongamos que en total existen n primos.

Podríamos darle un nombre a cada primo:

Al primero le llamamos p1, al segundo p2, al tercero p3, y así sucesivamente hasta lelgar al último primo pn.

Supongamos que ya hemos hecho esto.

Ahora, construyamos el número siguiente, al que llamaremos N, y que es

Es decir, calculamos el producto de los n primos y sumamos 1 

al resultado.

Ahora, vamos a ir dividiendo N entre todos los primos, uno por uno,

 y comprobamos si el resultado es entero:


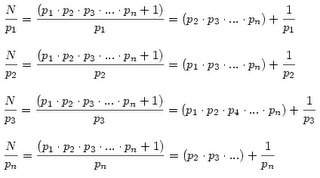
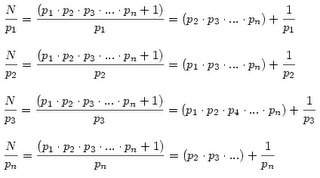
Vemos que en todos los casos por cociente tenemos un entero, el producto

 de todos los primos menos por el que estamos dividiendo, más un término

 del tipo 1/pn, que evidentemente no es entero:

ninguno de los cocientes de arriba es entero.

Por tanto, N no es divisible por ningún primo.

Solamente es divisible por si mismo, y la unidad*.

Luego N es, según 

la definicion anterior, un número primo.

Pero habíamos supuesto que en nuestra lista p1, p2, p3...pn

 estaban todos los primos.

Obtenemos así una contradicción 

Por tanto, como dijimos antes, nuestra premisa inicial es falsa y su contraria (hay infinitos números primos) es verdadera.

 Y ya hemos terminado.

La demostración parece larga, pero en realidad no lo es tanto,

 he aprovechado también para definir los números primos 

y para explicar las bases de la demostración por reducción al absurdo.

Espero que les haya resultado interesante.

*Si un número no es divisible por ninguno de los primos inferiores a el, tampoco lo es por ningún número inferior a el, ya que cualquiera de estos nímeros puede expresarse como producto de factores primos.

**La "auténtica" demostración de Euclides es ligeramente distinta

a la versión que doy aquí.

Creo que esta es más fácil de entender para el lector ocasional.