Mecánica cuántica from a dummy. Que no te lo cuenten 7 - Cuentos Cuánticos.

En la anterior entrada de este minicurso estuvimos jugueteando con dos operadores  y .  De esos operdores habíamos aprendido que eran hermíticos (por lo tanto es posible que describan observables físicos) y que su conmutador era distinto de cero.

Es decir, esos operadores no conmutaban y habíamos dicho que eran incompatibles entre sí.  En esta breve entrada vamos a discutir la importancia de la conmutación de operadores que describen observables físicos que es una de las piedras angulares de toda la problemática con la mecánica cuántica.

Pasen y vean.

Por cierto, no desesperen, en breve terminamos con esto y continuamos con el entrelazamiento y las desigualdades y todas esas cosas chulas.

Conmutar o no conmutar, that is the question

Como hemos comentado y como se calculó en la entrada anterior, los operadores que representan la característica color en la dirección 1 y 2 de nuestra caja no conmutan entre sí.

Eso implica muchas características de esas sorprendentes de la cuántica.

 Así que atentos a lo que sigue porque es un punto importante de todo esto que estamos haciendo.

Refresquemos la memoria.

Si queremos saber si dos operadores conmutan o no hay que calcular el conmutador entre ellos.  

La operación del conmutador se representa con los dos operadores de interés metidos entre corchetes cuadrados [ , ].

  Por supuesto, hemos de conocer la forma de los operadores y su actuación sobre los estados para poder calcular el conmutador:

Entre nuestros operadores el conmutador da una combinación de estados negros y blancos en la dirección 1 (porque hemos expresado ambos operadores en términos de dichos estados, si hubiéramos hecho con los estados blanco y negro de la dirección 2 el resultado nos saldría en términos de dichos estados 2)

Lo que podemos decir es que los operadores color en la dirección 1 y la dirección 2 no conmutan entre sí.

¿Por qué importa esto?  Resulta que cuando dos operadores no conmutan entre sí hay una serie de teoremas matemáticos que influyen mucho en la física que podemos describir con dichos operadores (recordemos que representan observables físicos).

Tus propios no son mis propios

Como hemos repetido ya muchas veces dado un operador siempre podemos encontrar sus estados propios, es decir, aquellos estados que tras la actuación del operador sobre ellos se quedan igual salvo que pueden ser multiplicados por un número.  Ese número es el valor propio del estado propio correspondiente para el observable que estemos considerando.

Para los operadores  y  conocemos sus estados propios correspondientes:

Ahora bien, lo que nos dice la matemática es que si dos operadores no conmutan no pueden tener los mismos estados propios.

Eso está muy claro en nuestro caso porque hemos sido capaces de expresar los estados propios blanco y negro en la dirección 2 en términos de los estados propios blanco y negro en la dirección 1 (por supuesto se pueden expresar los de 1 en términos de los de 2).

Es muy fácil ver que esos estados no son propios de .  Si hacemos actuar sobre ellos el resultado cambia, el estado resultante no es el original sobre el que ha actuado (multiplicado todo por un número) por lo que no es un estado propio de ese operador.  Pasaría la situación análoga si expresamos los estados propios de  en términos de los estados propios de .

Evidentemente aquí no estamos probando el teorema solo estamos viendo un ejemplo concreto en el que el teorema se realiza. Tenemos dos operadores que no conmutan cuyos respectivos estados propios no son propios del otro operador.

La importancia en física. Cuestión de indeterminación

Todo está muy bien pero en física lo que importa es si podemos predecir el resultado de las medidas o no podemos. Y claro, la cuántica se muestra un tanto especialista en ese sentido porque establece que los resultados de las medidas de un observable físico no pueden ser cualquier valor. 

 ¿Qué valores podemos obtener de un observable físico? 

 Lo que nos dice la cuántica es:

Los únicos resultados posibles de la medida de un observable físico son los valores propios asociados a los estados propios del operador matemático que represente al observable físico de interés.

Eso quiere decir que si medimos el color en la dirección 1 solo podremos obtener dos resultados (+1) para blanco y (-1) para negro.  Si el estado que queremos medir ya es el estado blanco en la dirección 1 el resultado está claro, obtendremos (+1)(Blanco) en la medida. Si introducimos un estado superpuesto no sabremos lo que obtendremos en una medida individual pero seguro que es blanco (+1) o negro (-1). 

No hay otras opciones.

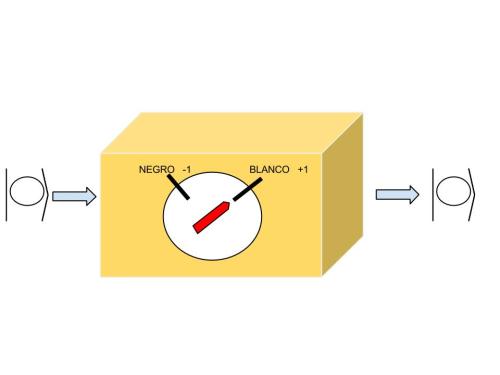
Medida sobre un estado propio del observable que estamos estudiando.

Medida sobre un estado superpuesto no propio. No podemos predecir las medidas individuales pero seguro que sale blanco o negro como resultado final. Así lo exige la cuántica.

Pero aquí viene el meollo de la cuestión.  Dado que  y  no conmutan no comparten estados propios.  Pensemos sobre ello un momento, ¿qué puede significar eso respecto a los resultados de las medidas?

¿Qué pasa si quiero medir sobre el estado blanco en la dirección 2 tanto  como ?  La cuántica nos dice que no están definidos esos valores simultáneamente ya que el estado no es propio de los dos operadores a la vez, de hecho, no existen estados propios simultáneos de ambos operadores.

¿Les recuerda a algo eso de que no se pueden determinar dos valores a la vez de dos magnitudes físicas?  

Espero que sí, espero que se acuerden del principio de indeterminación que discutimos en las primeras entradas de este minicurso en el bloque 1.

Siempre se nos dicen que hay pares de magnitudes físicas que no están determinadas a la vez. 

¿Quién determina esos pares de magnitudes que verifican un principio de indeterminación?  

Pues sí, supongo que lo vais intuyendo, eso se identifica mirando si los operadores que representan a los observables físicos conmutan o no.

Si conmutan pueden compartir estados propios y por lo tanto podemos medir simultáneamente esos observables porque nos darán una respuesta (no sabemos cual de los valores propios exactamente) uno de los estados propios comunes simultáneamente a ambos.

Si no conmutan no existen esos estados propios comunes por lo que si determinamos el valor de uno de los observables el otro queda totalmente indeterminado.  Eso es porque no hay ningún estado que tenga información simultánea sobre ambos observables a la vez. 

Ese es el meollo de la indeterminación cuántica.

Pensemos un ratito sobre ello.  Por ejemplo pensemos que el estado blanco en la dirección 2 tiene un color definido en la dirección 2, pero ¿qué color tiene para la dirección 1?  

Miremos de nuevo ese estado blanco en la dirección 2 expresado en términos de los estados propios de color de la dirección 1:

¿Está claro?  Supongo que no, pero esto es cuántica, nadie dijo que fuera fácil :P

Nos seguimos leyendo…