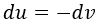
La solución de Schwarzschild:

Espacio-tiempo de Schwarzschild. La singularidad (roja) es la recta asociada a r=0. El horizonte de sucesos es la línea negra asociada a r=rs. Los rayos de luz saliendo y entrando del horizonte son, por ejemplo, las líneas amarillas que salen a 45º del origen de coordenadas. Se nota que junto al mismo se mueven más despacio (menor avance espacial). La línea azul representa el contorno de una esfera envolviendo al horizonte y la línea verde es un ejemplo de isocrona.
Recapitulemos. En la solución de Schwarzschild usábamos para describir el espacio-tiempo cuatro coordenadas elementales: el tiempo t, la distancia al origen de coordenadas r, y los ángulos latitudinal y longitudinal. El tiempo y el radio r, respectivamente, podían tomar los siguientes valores:
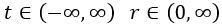
Teniendo esto en cuenta, la expresión para el tiempo propio τ cumplía:
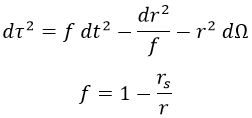
Aquí englobamos en dΩ todos los movimientos angulares.
Para un rayo de luz con movimiento exclusivamente radial se cumplía:
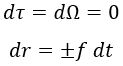
La coordenada “tortuga”:

La coordenada tortuga no abarca el horizonte ni la singularidad, y las formas del resto de líneas son análogas al espacio vacío.
Es posible obtener una forma más agradable para la expresión del tiempo propio usando la coordenada “tortuga” r*, que tiene la propiedad de barrer exclusivamente el espacio fuera del horizonte de sucesos y no representar su interior. Su definición es la que sigue:

Se puede obtener una expresión analítica para la misma integrando:
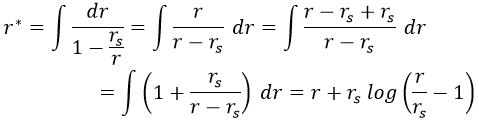
Y aquí se aprecia lo que anticipábamos. Cuando r es nulo, la coordenada tortuga es compleja, con lo que no lo abarca. Cuando r es rs, es decir, el horizonte de sucesos, la coordenada tortuga vale -∞. De ahí, en adelante, la coordenada tortuga crece con normalidad hasta el infinito. Esto hace que el espacio de configuración pase a ser:
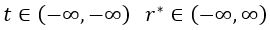
La coordenada tortuga tiene un rango de valores más amplio, pero representa menos espacio.
Tengamos ahora en cuenta la siguiente igualdad:
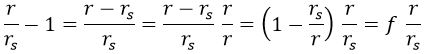
Podemos usarla para, junto con la expresión de la coordenada tortuga, obtener otra expresión de f:
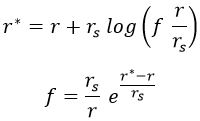
Esto nos deja la ecuación del tiempo propio del siguiente modo:
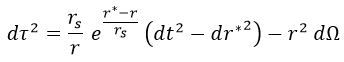
En este sistema de coordenadas, los rayos de luz radiales siguen trayectorias rectas de pendiente 1, o lo que es lo mismo, de 45º exactos en todas partes:
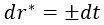
Por otra parte, la coordenada tortuga es compleja para la singularidad (0) e infinitamente negativa para el horizonte:
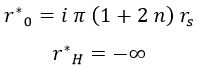
Coordenadas cono luz:

A efectos prácticos, giramos la gráfica de la coordenada tortuga 45º a la derecha.
Una vez introducida la coordenada tortuga, podemos hacer un cambio a coordenadas cono luz u y v, ya vistas en otra ocasión bajo otro nombre, para que las cuentas siguientes resulten más sencillas. El cambio a estas coordenadas cono luz es, salvo un factor de escala, equivalente a rotar todas las figuras 45º a la derecha o, equivalentemente, rotar los ejes 45º a la izquierda:
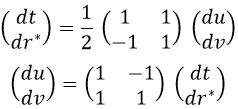
Es fácil comprobar que haciendo esto preservamos el dominio:
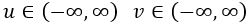
Aquí evidentemente se cumple:
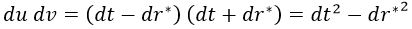
Y que la métrica toma la forma:
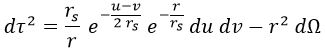
En este caso, los rayos de luz radiales son paralelos a los ejes coordenados, al tener que cumplir que o u o v sean constantes:
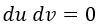
El horizonte se sucesos sigue quedando fuera del rango de las coordenadas, en esta ocasión infinitamente arriba y a la izquierda:
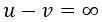
Las isocronas, por su parte, en este sistema de coordenadas son rectas con pendiente -1:
Coordenadas Kruskal:
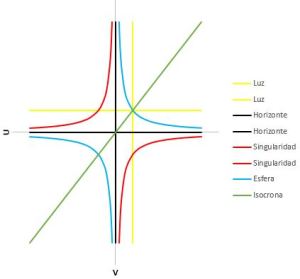
Las coordenadas Kruskal traen el horizonte de sucesos a los ejes U y V, y la singularidad es una hipérbola roja en el segundo y cuarto cuadrante. La esfera envolviendo al agujero negro pasa a ser otra hipérbola en las regiones exteriores y aparecen un universo alternativo en el tercer cuadrante y un agujero blanco en el cuarto. Los rayos de luz siguen trayectorias paralelas a los ejes, saliendo siempre del agujero blanco o acabando en el agujero negro, a excepción de las trayectorias congeladas en el horizonte. Las isocronas son rectas que pasan por el origen. Hemos representado la isocrona 0. Yendo infinito tiempo hacia atrás (girando 45º a la derecha) nos encontramos con el horizonte blanco. Yendo infinito tiempo hacia delante nos encontramos con el horizonte negro. En el universo paralelo de la región tres el tiempo contrario, hacia el “agujero blanco”, con lo que ambos universos tienen un flujo temporal invertido.
Una vez ubicados en el sistema cono luz, procedemos a traer el horizonte de sucesos y la singularidad desde el infinito a una región visible en el diagrama. Para ello, definimos los parámetros U y V tales que lo que antes estaba en infinito ahora esté en 0 y lo que antes era complejo (la singularidad) ahora sea negativo. Lógicamente, para ello tiraremos de logaritmos y exponenciales:
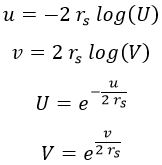
Como aceptamos valores complejos de u y v, obtenemos que de nuevo U y V pueden abarcar todo el plano:
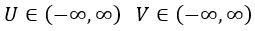
Para obtener la métrica en su nueva forma, es conveniente hacer las siguientes operaciones:

Con lo que:
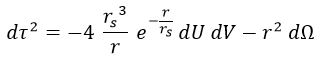
Cabe destacar que la métrica, en lo que a dU dV respecta, es proporcional a la métrica con du dv. Esto va a implicar que todos los ángulos relativistas se van a preservar y las rectas cuyos vectores directores fuesen perpendiculares en coordenadas cono luz también serán perpendiculares (en sentido minkowskiano) en coordenadas Kruskal.
En efecto, la ecuación de los rayos de luz es análoga:
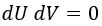
Observemos ahora que se cumple lo siguiente:
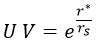
Para una distancia r* dada, la figura con la que será descrita su esfera asociada en el plano Kruskal será una hipérbola o una recta, tal y como se puede verificar con un análisis de ecuaciones cuadráticas en el plano.
Concretamente, la singularidad, a la cual correspondía una coordenada tortuga compleja, da como resultado una hipérbola tras aplicar la ecuación de Euler para números complejos:
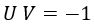
Cabe destacar que como la hipérbola tiene dos ramas, aparece una segunda curva singular asociada a un “agujero blanco” abajo a la derecha. Las trayectorias que surgen en el agujero negro salen siempre del horizonte de sucesos hacia fuera, y las que entran en el mismo acaban en el agujero negro habitual.
El horizonte de sucesos, por su parte, serán los propios ejes coordenados:
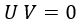
Dichos ejes dividen el espacio-tiempo en dos regiones fuera del agujero negro aisladas y que no pueden comunicarse de ningún modo: el primer y el tercer cuadrante. Nosotros en principio trabajaremos solo con el primero, pero si un observador del universo alternativo del tercer cuadrante atravesase el horizonte de sucesos podría coincidir con otro nuestro allí. Es decir: dos mundos causalmente desconectados podrían estar conectados mediante agujeros negros.
En lo referente a las isocronas, podemos adaptar la ecuación diferencial de las mismas en coordenadas cono luz a las coordenadas Kruskal e integrar:
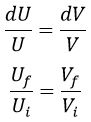
Lo que se puede reescribir diciendo que las isocronas son trayectorias en las que se mantiene constante el cociente entre U y V, o lo que es lo mismo, que son rectas que pasan por el origen de coordenadas:
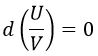
Coordenadas Carter-Penrose cono-luz:
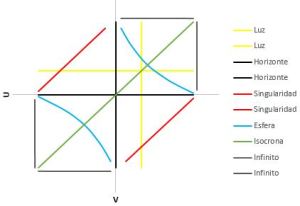
Las singularidades pasan a ser líneas rectas y el infinito pasa a estar visible, siendo las dos líneas rectas que delimitan los cuadrantes primero y tercero.
Después de traer la singularidad a un lugar visible, lo último que queda por hacer es traer también el infinito, la distancia más lejana a la singularidad, a un lugar visible. Esta transformación, por supuesto, fue idea de matemáticos, entre ellos el famoso Roger Penrose, y se realiza de una forma muy sencilla utilizando tangentes y arcotangentes:
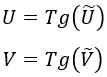
Con esto conseguimos reducir el dominio infinito de las coordenadas Kruskal a algo mucho más acotado:
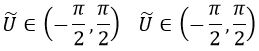
Para obtener la métrica nueva, solo tenemos que tener en cuenta las siguientes relaciones:
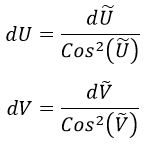
Con lo que obtenemos de nuevo una transformación que preserva ortogonalidad relativista:
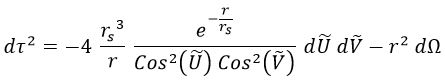
Obviamente los rayos de luz radiales continúan siguiendo trayectorias paralelas a los ejes coordenados, y con las hipérbolas sucede algo sorprendente. La ecuación geométrica pasa a ser:

Esto hace que la singularidad venga descrita por la ecuación:
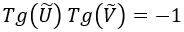
Que puede parecer una ecuación complicada de representar, pero en realidad se reduce fácilmente a rectas como:

Ya que:
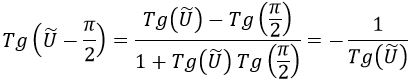
De modo que las hipérbolas singulares pasan a ser rectas de pendiente unidad.
El horizonte de sucesos cumple la ecuación:
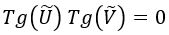
Pero esto no incluye ninguna novedad, ya que las solución siguen siendo los ejes coordenados.
Con respecto a las isocronas, tiene que cumplirse:
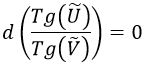
Lo cual distorsiona la idea de rectas que pasen por el origen, siendo la única que aguanta sin deformarse la de 45º.
Coordenadas Carter-Penrose:

Un giro de 45º del diagrama con coordenadas cono luz.
Por último, una vez hecha toda la aventura, solo queda deshacer el sistema cono luz para que los ejes queden más adecuadamente orientados. Esto se consigue, obviamente, mediante una transformación del estilo:
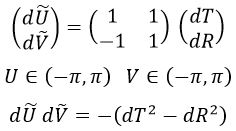
Con lo cual giramos el sistema de nuevo 45º a la derecha y obtenemos la métrica de Carter-Penrose:
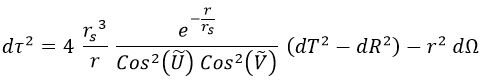
Y en esto consiste, básicamente, hacer un diagrama de Carter-Penrose para un cierto espacio-tiempo.
Diagrama de Carter-Penrose para el agujero negro de Reissner-Nordström:
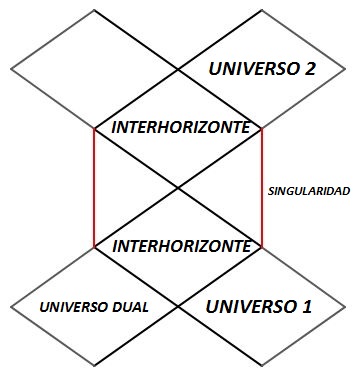
En el caso del agujero negro cargado, recordemos que la función f se anulaba en dos valores de r denominados horizonte interno r- y horizonte externo r+. Esto implica que existirán dos coordenadas tortuga diferentes según si queremos abarcar el universo exterior del agujero negro cargado o el interior. La singularidad, por otra parte, no estaba entre los dos horizontes, sino en el universo interno. Esto permite desarrollar un diagrama montando los asociados a las dos coordenadas tortuga de forma que encajen a la perfección y representen una multitud de universos conectados causalmente mediante los horizontes interno y externo.
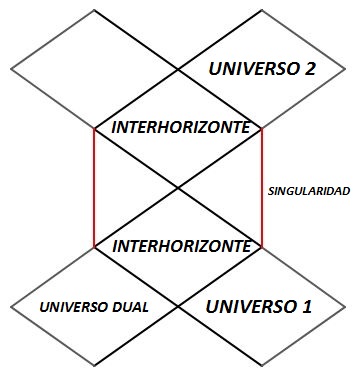
Diagrama del agujero negro de Reissner-Nordström. A través del interhorizonte (región entre los dos horizontes), se puede llegar al interior del agujero negro, y a partir de ahí o bien acabar en la singularidad o bien volver a entrar en el interhorizonte para aparecer en un universo nuevo.