Hasta ahora, aplicando la relatividad general, hemos obtenido solo dos de sus soluciones conocidas: el agujero negro de Schwarzschild y la cosmología de Friedmann. En el caso del primero, analizamos el problema en 3 dimensiones y obtuvimos un resultado que, si bien correcto, no era el adecuado para extrapolar conclusiones a 4 dimensiones.
En esta entrada obtendremos el campo gravitatorio creado por un agujero negro esféricamente simétrico y cargado con una cierta carga Q, conocido como la solución de Reissner-Nordström y descubierto en 1918, poco después del primero. Para ello, volveremos a obtener el tensor de Ricci en una geometría estática y esféricamente simétrica en el caso de 4 dimensiones y lo aplicaremos en dos situaciones: cuanto la energía del espacio es exclusivamente debida a la masa del agujero negro y cuando es debida a un campo eléctrico radiado por el agujero negro.
Como conclusión, veremos que el campo electrostático gravita y que altera los efectos gravitatorios, además de producir sus efectos habituales.
El tensor de energía-momento a partir de la lagrangiana relativista de una masa:
Como ya sabemos, la acción relativista S de un sistema viene dada por la integral de su lagrangiana en el tiempo propio τ;
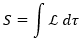
En el caso de una partícula de masa m, dicha lagrangiana depende de la cuadrivelocidad U y del campo gravitatorio g en el espacio:
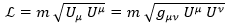
Siendo esta su lagrangiana, si dicha partícula está encerrada en un volumen V le corresponden el siguiente cuadrimomento p y tensor energía-momento T:
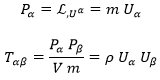
Aquí ρ sería la densidad de la partícula en su volumen.
¿Es posible obtener el tensor de energía-momento mediante una relación directa con la lagrangiana? Sí, pero para ello es más razonable emplear la densidad lagrangiana (por unidad de volumen):
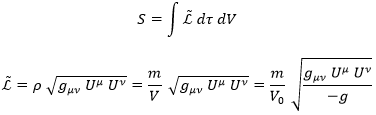
En el último paso cambiamos el elemento de volumen V distorsionado por el campo gravitatorio por según el volumen euclídeo V0 multiplicado por la gravedad raíz(-g), una expresión cierta localmente (para pequeños desplazamientos). Esa g sería el determinante del campo.
Teniendo esto, siempre es cierto que el tensor energía-momento cumple:
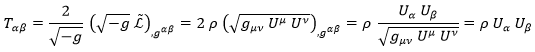
Nótese que la densidad depende del punto del espacio y no tiene por qué ser constante.
Y teniendo este tensor y su traza T podemos usarlo en la ecuación de Einstein directamente:
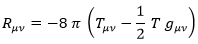
El tensor de Ricci en 4 dimensiones con simetría esférica:
Cuando resolvimos el problema en 3 dimensiones vimos que el campo gravitatorio en coordenadas esféricas solo alteraba las medidas temporales y las medidas en la dirección radial. Además vimos que una distorsión era inversa y opuesta a la otra. Aplicando dicha relación, podemos partir de que el campo gravitatorio será de la forma:
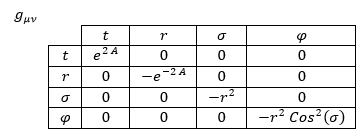
Por otra parte, el campo gravitatorio en componentes contravariantes sería:
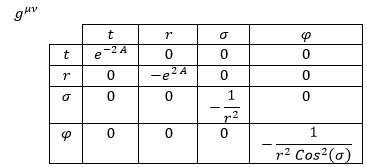
La derivada del campo sería (derivando respecto a las coordenadas por orden de lectura):
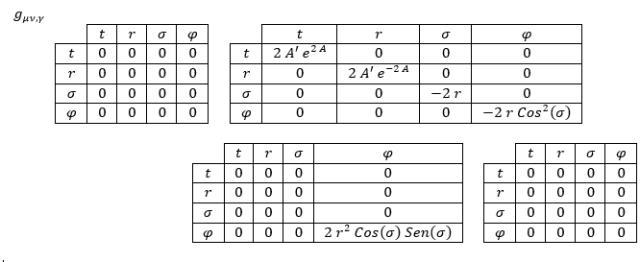
La conexión afín se obtendría de la forma usual, dando como resultado:
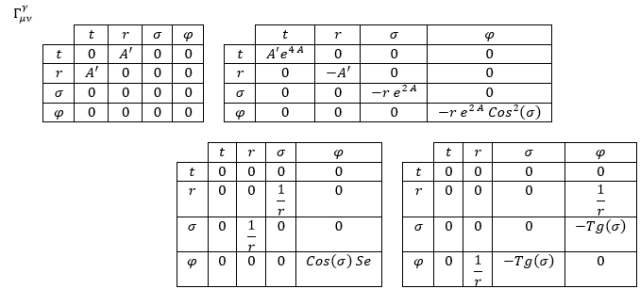
Y teniendo la conexión afín se obtenía el tensor de Ricci del siguiente modo:
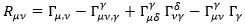
La conexión contraída tiene la siguiente expresión:
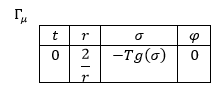
El primer término del Ricci es:
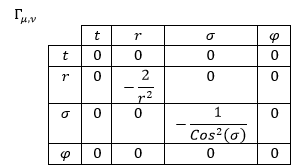
El segundo término es:

El tercer término es:

Y el cuarto término es:
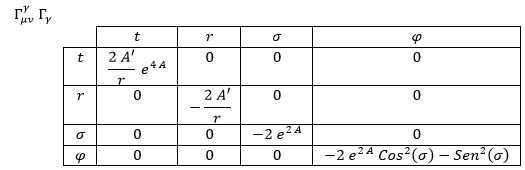
Y combinando todo, el Ricci es:

Cabe destacar que sus últimas dos componentes se pueden reescribir aplicando la derivada del producto a la inversa:
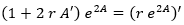
Así como que de sus cuatro componentes, realmente solo dos son independientes porque se cumple:
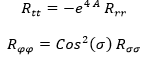
Normalmente habría tres componentes independientes, pero hemos fijado al usar que sabíamos la forma de la métrica más o menos.
La solución de Schwarzschild:
En el agujero negro de Schwarzschild imponíamos que el tensor de Ricci fuese nulo en todas partes menos en el origen de coordenadas:
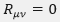
Esto se traduce en dos ecuaciones independientes que se deben cumplir simultáneamente:
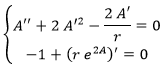
Así, obtenemos la métrica usando la segunda ecuación y posteriormente se puede comprobar que la primera también se cumple con la misma solución:
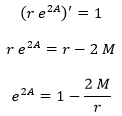
Aquí, al integrar en el primer paso hemos fijado la constante de integración como -2M aplicando el criterio fundamental de la relatividad general sobre la forma que debe tener el campo gravitatorio a una cierta distancia.
Como se puede ver, la solución obtenida es la ya conocida métrica de Schwarzschild. Nótese que esa exponencial era la distorsión temporal del campo gravitatorio tal y como la hemos introducido aquí.
La ley de Coulomb en campo gravitatorio:
Como ya vimos en su momento, la lagrangiana del campo electromagnético libre es:
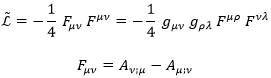
Aquí F sería el campo electromagnético propiamente dicho y A el cuadripotencial.
Si denotamos por E al campo eléctrico radial, que será el único con el que dotaremos a nuestro agujero negro cargado, y la métrica es la esféricamente simétrica, se cumplen las siguientes igualdades:
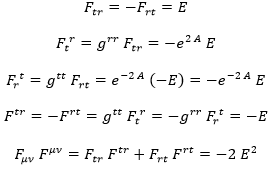
Por otra parte, el campo electromagnético libre (en ausencia de cargas), cumple que su gradiente es nulo:
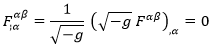
Donde se cumple que:
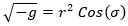
Con lo cual:
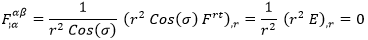
Y de la última igualdad podemos despejar el campo E, verificando que pese al campo gravitatorio del agujero negro se sigue cumpliendo la ley de Coulomb:
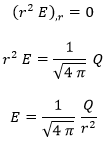
De nuevo hemos elegido la constante de integración a conveniencia en el primer paso.
La expresión poco habitual es debida a que tratando con agujeros negros cargados se suele fijar, con el espíritu de las unidades naturales, que:
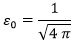
Yo soy más partidario de hacer esta igualdad sin la raíz, y así lo he hecho en todas las entradas hasta ahora, pero es innegable que el problema que nos ocupa será más sencillo de este modo.
El tensor energía-momento del campo electromagnético:
Para obtener el tensor energía-momento, usamos la expresión que depende de la lagrangiana:
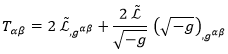
En el segundo término, tenemos la derivada del determinante del campo respecto al campo. Para obtener tal cosa, usamos la siguiente relación:
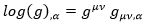
Desarrollando la derivada del logaritmo del determinante a la izquierda y despejando, se obtiene la derivada de un determinante:
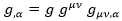
Y a partir de aquí podemos obtener la derivada que queremos teniendo en cuenta la derivada de una raíz:
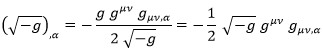
De modo que:
Donde en la segunda igualdad usamos dos deltas de Kronecker para expresar la derivada del campo con unos índices con respecto al campo teniendo otros.
Sustituyendo en la ecuación del tensor de energía-momento:
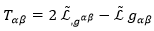
Centrémonos ahora en el primer término. El campo electromagnético no se puede derivar parcialmente respecto al campo gravitatorio porque no depende de él, de modo que esas derivadas nos las ahorramos y aplicando la derivada del producto resulta:
De modo que sustituyendo esto y expresando lo que podemos en función de la carga tenemos que el tensor energía-momento es:
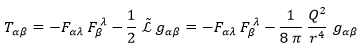
Y que su traza es nula:
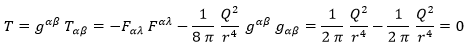
Debido a este último hecho, con el campo electrostático presente la ecuación de Einstein a resolver será:
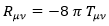
Donde las componentes del tensor energía-momento se calculan usando la fórmula obtenida:
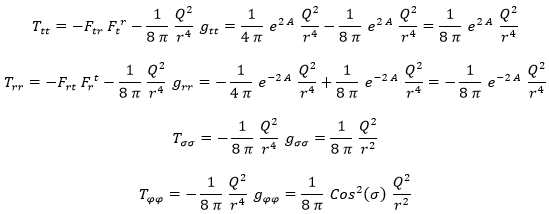
O escrito de otra forma:

Aquí se observa que sus componentes cumplen las mismas relaciones entre ellas que el tensor de Ricci:
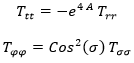
La solución de Reissner-Nordström:
Usando la ecuación de Einstein descrita unas líneas arriba y teniendo en cuenta que solo dos componentes del campo son independientes, tenemos que resolver el siguiente sistema:
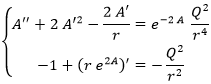
De donde aplicando la misma filosofía que en el caso de Schwarzschild obtenemos:
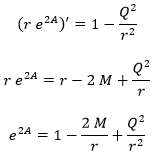
Es decir, que un agujero negro con campo eléctrico tiene una carga efectiva cuyo efecto se opone al de la masa, pero también se atenúa más rápido.
En la próxima entrada veremos que un agujero negro cargado tiene dos horizontes, lo que dio lugar por primera vez a la especulación de que podría ser útil para realizar viajes en el tiempo.