A cada estado de un sistema físico le asignaremos un elemento de un espacio virtual complejo H
(espacio de Hilbert), de dimensión N.
Normalmente N tiende a infinito.
Esto será de ayuda ya que conocemos como funcionan los espacios vectoriales.
Llamaremos a cada elemento “ket” y lo representaremos por
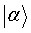
. Denotaremos un espacio dual H* formado por los mismo elementos de H, pero conjugados, llamados “bra”
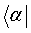
.
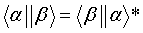
Definimos el producto escalar como:
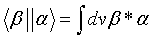
= un nº complejo
Definimos observable como toda magnitud que se puede medir, y las representaremos mediante operadores.
Por ejemplo siendo el operador A:
Si
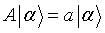
llamaremos a a (nº) autovalor de A y alfa autofunción o autovector del operador A.
El conjunto
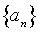
se llamará espectro. Si ocurre que 2 o mas autoestados tienen
el mismo autovalor se dice que el
operador tiene espectro degenerado. Por ejemplo:
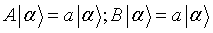
degeneración de orden 2
Se define operador adjunto: A*, siendo el correspondiente de A en el espacio dual. Si A=A* A se llama hermético.
Los autovalores de los operadores herméticos son reales.
Los autovalores de un operador son ortogonales, es decir:
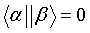
Por construcción H está generado por el conjunto de autovectores, es decir el conjunto de autovectores es una base. De esta manera podemos representar cualquier otro elemento como combinación
lineal de estos elementos:
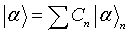
Se define conmutador de 2 operadores como
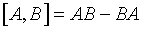
. Esta igualdad
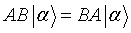
no tiene porque ser cierta, lo será sólo en el caso de que el conmutador sea igual a 0. Si el conmutador es igual a 0, A y B tienen los mismos autovectores, es decir tienen una base común.
Se define el valor medio de un operador como:
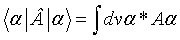
. El error cometido en el valor medio se llama dispersión de un operador y se calcula como
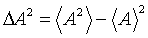
Cuando una magnitud física viene representada por un operador, el resultado de una medida de esa magnitud sólo puede ser un autovalor del operador correspondiente.
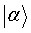
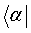
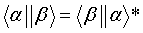
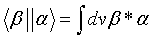
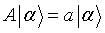
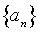
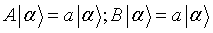
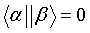
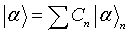
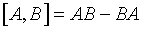
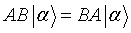
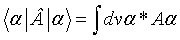
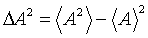
No hay comentarios:
Publicar un comentario