Derivation from Determinant
We assume that n is an even number and A = (aij) is an 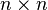 skew-symmetric matrix.
skew-symmetric matrix.
The Pfaffian of A can be derived as follows. Using the Laplace's formula we can write det(A) as

where Cij = ( − 1)i + jdet(Aij) is the ijth cofactor of A and Aij is the ijth minor of A. By the adjugate formula, we have

We have

Thus

where  is the
is the  minor of A obtained by deleting the first two rows and the first two columns of A. Of course, it is arbitrary that we have changed the first two rows in the above equation. In general we have
minor of A obtained by deleting the first two rows and the first two columns of A. Of course, it is arbitrary that we have changed the first two rows in the above equation. In general we have

So far we have not used the assumption that n is even and A is skew-symmetric. With that, since Aii is an  skew-symmetric matrix and (n − 1) is odd, clearlydet(Aii) = 0 and hence Cii = 0. Similarly Cjj = 0. On the other hand,
skew-symmetric matrix and (n − 1) is odd, clearlydet(Aii) = 0 and hence Cii = 0. Similarly Cjj = 0. On the other hand,

So the above equation is simplified as
 .
.
We now plug this back into the original formula for the determinant,

which yields

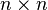 skew-symmetric matrix.
skew-symmetric matrix. 



 is the
is the  minor of A obtained by deleting the first two rows and the first two columns of A. Of course, it is arbitrary that we have changed the first two rows in the above equation. In general we have
minor of A obtained by deleting the first two rows and the first two columns of A. Of course, it is arbitrary that we have changed the first two rows in the above equation. In general we have
 skew-symmetric matrix and (n − 1) is odd, clearlydet(Aii) = 0 and hence Cii = 0. Similarly Cjj = 0. On the other hand,
skew-symmetric matrix and (n − 1) is odd, clearlydet(Aii) = 0 and hence Cii = 0. Similarly Cjj = 0. On the other hand,
 .
.

No hay comentarios:
Publicar un comentario