sábado, 22 de junio de 2013

¿Por qué domina la materia?

Al principio el universo está dominado por fotones, y estos producen pares de partícula/antipartícula:
\gamma +\gamma \rightarrow p +\bar{p}
Pero como ya hemos dicho esto daría la misma cantidad de materia que de antimateria.  Pero esto, evidentemente no pasó.
Sakharov nos da la clave:
Como hay que explicar esto pues hay que proponer escenarios que puedan explicar la existencia de materia en detrimento de la antimateria.  La mayor parte de la materia en el universo (al menos la visible) está en forma de bariones (que son las partículas que sienten la interacción fuerte compuestas por tres quarks, los ejemplos más comunes son los protones y los neutrones).  Entonces Sakharov propone tres condiciones que tiene que cumplir una teoría para explicar esta asimetría:
Tiene que existir un mecanismo que viole la conservación del número bariónico
Groso modo esto significa lo siguiente:  En las reacciones entre partículas se conserva el número barionico (El número barionico de los bariones será positivo y el de los antibariones negativo). 
 El número bariónico inicial en una reacción será igual al final, en situaciones normales.
La interacción presente ha de violar C y CP.
Recordemos, P cambia el sentido de los vectores (posiciones, momentos) pero no cambia el momento angular (ni por tanto el espín).  C cambia la carga por su opuesta.  CP por tanto conecta una partícula con su antipartícula.
Aclaración:
Se habla del espín de las partículas, que por ahora consideraremos que representa un hipotético giro de las partículas (no lo es, pero la analogía es espectacularmente buena).  Y decimos que el electrón tiene espín 1/2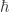\hbar.  Pero en realidad lo que nos interesa de una partícula no es simplemente su espín.  En realidad, lo interesante es la proyección del espín en la dirección del momento lineal (en la dirección del movimiento).  Por tanto, la transformación P (cambia el sentido de movimiento pero no el espín) lo que hace es cambiar esta proyección.

La situación donde se produce la asimetría materia/antimateria no puede ser de equilibrio termodinámico.
Esto es natural, porque una situación de equilibrio implicaría reversibilidad de las condiciones y no podríamos tener exceso o defecto de materia, porque si revertimos el proceso no llegaríamos a la situación inicial.
Estás son las conocidas como condiciones para la bariogénesis.  Y por supuesto no son la única elección de condiciones para producir esto, por ejemplo podemos encontrar las condiciones de Weinberg (pero esa es otra historia).
¿Qué significa que un proceso viola CP?
Lo interesante de CP es que nos dice que si una partícula se desintegra en otras partículas.  La antipartícula tiene que hacer exactamente lo mismo pero en la “antidesintegración” (cambiando todas las partículas por las propias antipartículas y viceversa).
En general, una partícula puede decaer de varias formas (siempre que se respeten las leyes de conservación).  Así que su antipartícula decaerá de las mismas formas.  El que se decaiga en una determinada forma, lo que se llama en un determinado canal, viene dado por una probabilidad.  Entonces CP relaciona las probabilidades de los canales de desintegración de partículas y antipartículas.
¿Me pones un ejemplo?
Introduzcamos a nuestro amigo el Kaon:
Representación del contenido quark de algunos hadrones. Está representado el kaón neutro.
El kaón esta compuesto por un quark y un antiquark (evidentemente no del mismo tipo porque entonces se desintegrarían).  Los compuestos quark-antiquark se llaman mesones.
Además el kaón es el mesón más ligero que contiene un quark extraño (s).  Pero el kaón se desintegra (decae) a partículas más ligeras.  Y esto es sorprendente, ¿por qué?  Pues porque la interacción fuerte preserva el sabor (el tipo) de los quarks. Es decir, que si empiezo con un quark s, por interacción fuerte debería de acabar al final con un quark s.  Pero el kaón no puede hacer eso, porque no hay partícula más ligera que él mismo que contenga un quark s.  Así pues el kaón decae por interacción débil (que lo que hace, esta sí, es cambiar el sabor de las partículas).
Entonces, podemos escribir el kaón (neutro) |K^0\rangle  y el antikaón neutro |\bar{K^0}\rangle. 
 Pero también podemos identificar estados mezclados que tienen propiedades interesantes bajo transformaciones CP:
|K^0_1\rangle=\frac{1}{\sqrt{2}}(|K^0\rangle +|\bar{K^0}\rangle)
|K^0_2\rangle=\frac{1}{\sqrt{2}}(|K^0\rangle -|\bar{K^0}\rangle)

Es fácil ver que CP cambia $|K^0\rangle \rightarrow |\bar{K^0}\rangle$ y viceversa.
Apliquemos ahora CP a |K^0_1\rangle y |K^0_2\rangle:
CP\left[|K^0_1\rangle=\frac{1}{\sqrt{2}}(|K^0\rangle +|\bar{K^0}\rangle)\right]=
CP |K^0_1\rangle=\frac{1}{\sqrt{2}}(CP|K^0\rangle +CP|\bar{K^0}\rangle=
CP |K^0_1\rangle=\frac{1}{\sqrt{2}}(|\bar{K^0}\rangle +|K^0\rangle=|K^0_1\rangle

Entonces diremos que |K^0_1\rangle tiene CP +1
CP\right[|K^0_2\rangle=\frac{1}{\sqrt{2}}(|K^0\rangle -|\bar{K^0}\rangle)\left]=

CP |K^0_2\rangle=\frac{1}{\sqrt{2}}(CP|K^0\rangle - CP|\bar{K^0}\rangle=

latex CP |K^0_2\rangle=\frac{1}{\sqrt{2}}(|\bar{K^0}\rangle -|K^0\rangle

CP|K^0_2\rangle = -\frac{1}{\sqrt{2}}(|K^0\rangle -|\bar{K^0}\rangle)=-|K^0_2\rangle

Entonces diremos que K^0_2\rangle tiene CP -1.
Esto implica que dados |K^0_1\rangle y |K^0_2\rangle, 
sus desintegraciones no será iguales, porque su comportamiento bajo CP no es igual.
No entraremos en detalles, pero pondremos las reacciones preferidas de estas partículas, que decaen a piones:
K^0_1\rightarrow \pi \pi
K^0_2\rightarrow \pi\pi\pi

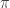donde \pi hace referencia a los piones.
Lo que está claro es que la segunda desintegración llega a un resultado con mayor masa que el resultado paraK^0_1, por tanto la desintegración para el K^0_2 es menos “efectiva”, o dicho de otro modo, la vida media de K^0_2 es 600 veces mayor que la del K^0_1.  Por eso al kaón 1 se le suele llamar corto (short en inglés) K_S y al kaón 2 largo (large en inglés) K_L.
¿Y cómo ver la violación de CP en este sistema?
Lo que se ha de verificar es que K_S\rightarrow 2\pi y K_L \rightarrow 3\pi.  
Pues bien, hagamos un experimento sólo con kaones largos y estudiemos sus desintegraciones.  
Este experimento fue hecho en Brookhaven y encontraron lo siguiente:
De 22700 desintegraciones alrededor de 45 de ellas fueron a dos piones.
Eso implica que hay una cierta preferencia por la materia que por la antimateria y que la interacción débil viola CP.
Desgraciadamente este método (por interacción débil) de generar la asimetría de interés no puede explicar toda ella.  Es decir, la asimetría que vemos entre materia y antimateria es mucho más severa de lo que se podría obtener por los planteamientos vistos en esta entrada.
Continuará…
Publicado por en