Física Rebelde: El problema de la jerarquía

La física, como todos, también tiene sus problemas con la jerarquía .

Pero, ¿qué entendemos por un problema con la jerarquía en este contexto?

Para empezar, digamos que el problema se puede parafrasear en esta pregunta:

¿Por qué la gravedad es tan débil?

Y aquí viene la pregunta del millón, ¿a qué es debido que una interacción sea más o menos intensa? 

 Y la respuesta es:  A su constante (constante de acoplo).

Todos habremos resuelto el típico problema de, tenemos dos masas de un kilo cargadas con un culombio cada una separadas un metro:

  ¿Qué fuerza es más grande la eléctrica o la gravitatoria?

Si uno hace las cuentas tendría que calcular .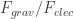  

Si sustituimos los datos del anterior problema tenemos:

así que el anterior cociente simplemente es G/K.  Si buscamos los valores y sustituimos pues ya tenemos la respuesta, G viene siendo un poquito menor que K.

Pero cuando hablamos del problema de la jerarquía nos referimos a un problema en las entrañas del modelo estándar.  En esta entrada procuraremos exponer qué y por qué es un problema esto de la jerarquía y dejaremos sus posibles soluciones (a cual más interesante) para otra entrega.

Acotación: Energías, Masas, Longitudes y Tiempos 

¿todos con las mismas unidades o sus inversas?

Durante esta entrada hablaremos de energías y masas en términos del electrón-voltio y sus múltiplos. Esta es una unidad de energía que se relaciona con los Julios de toda la vida del siguiente modo:

1 eV = 1,602176462 × 10-19 Julios

Pero se hace necesaria la explicación de por qué usamos unidades de energía para hablar de masas, longitudes y tiempo en lo tocante al modelo estándar y por extensión a toda la física de altas energías (o de partículas).

Cuando uno trabaja con partículas elementales es muy útil tener las dos constantes universales representativas como cantidades adimensionales (lo que equivale a redefinir las unidades con las que expresamos las medidas).

 En este ámbito, el de las partículas elementales, estamos tratando con fenómenos cuánticos que vienen regidos por la constante de Planck 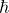 y la velocidad de la luz en el vacío .

Por lo tanto, Si decimos que  adimensional, estamos equiparando las siguientes dimensiones (recordemos que para expresar las dimensiones de una cantidad compuesta se pone entre barras):

 por tanto, en el sistema de unidades naturales:  y por tanto en estas unidades naturales (con c=1 adimensional) las dimensiones de Longitud y tiempo son equivalentes (lo cual es consistente con la relatividad).

Si decimos que 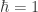 , estamos equiparando las dimensiones de las siguientes cantidades:

$|\hbar|=|E|\times T$ por tanto, en el sistema de unidades naturales:  así las dimensiones de energía son equivalentes a las dimensiones de inverso de tiempo (una frecuencia vamos).

Por último como ya han comentado: Empleando 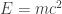 en unidades naturales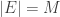 

Por eso es que en el sistema de unidades naturales, la masa se mide en unidades de energía, las longitudes y los tiempos en unidades de inversos de energía. 

Esto es realmente útil en física de partículas y simplifica la forma de dar los resultados teórico y experimentales.

Problema de la jerarquía en el modelo estándar

Bien, establezcamos un poco la estructura de las teorías.  Las teorías tienen un rango de aplicabilidad, dicho rango hace referencia a la escala de energías, (y por tanto longitudes y masas) en las cuales una teoría es fiable y da buenos resultados.

Así que imaginemos que tenemos una escala de energía que denotamos por .  

Esta escala delimita las teorías que construimos. 

 Si una teoría tiene un rango de aplicabilidad para energías menores que  hablamos de teorías a baja energía, si por el contrario otra teoría tiene un rango de aplicabilidad hasta energías mayores, hablamos de teoría a alta energía o extensión ultravioleta (esto es por razones históricas porque nosotros no podemos ver la luz a partir de esas frecuencias ultravioletas).

La física ha de ser consistente, entonces si tengo dos teorías donde una cubre los fenómenos físicos hasta  y la otra hasta energías superiores, está claro que ambas teorías han de dar explicación consistente a los fenómenos que ocurran por debajo de . 

 Por lo tanto, los parámetros de la teoría a baja energía (como las constantes de acoplo, las masas de las partículas que aparecen a esas energías, etc) tendrán que relacionarse con los parámetros correspondientes a la teoría de alta energía que la contiene.

Y aquí viene la jugada, en el modelo estándar tenemos una escala de energía que ronda los 100 Gev. (1GeV = eV), llamada escala electrodébil (energía por debajo de la cual electromagnetismo e interacción débil se hacen diferentes, por encima de ese valor de la energía son exactamente la misma interacción, están unificadas).  No pasa nada, pero resulta que hay otra escala en juego, y es la escala donde la gravedad se hace comparable en intensidad al resto de interacciones, a esta escala se le llama la escala de Planck (básicamente la masa de Planck expresada en eV).  Pero resulta que la escala de Planck está a GeV.  Así en un primer vistazo cualquiera diría que son bastante diferentes.

¿Dónde está entonces el problema? Tenemos dos escalas ¿y qué?

Para empezar tenemos un problema incómodo, nosotros hemos estudiado la gravedad clásica hasta el orden del centímetro (quizás hayamos llegado ya a bajar eso, pero tampoco nos pongamos tiquismiquis).  Y sabemos que la gravedad tiene poco que decir en la física de partículas porque es poco intensa, entonces, sólo se modificará a la escala de Planck.  Y tendremos unos bonitos 17 ordenes de magnitud donde estamos presuponiendo que la gravedad se comporta igual que en nuestra escala.  Cuanto menos es arriesgado.  Eso quiere decir que no hay nueva física por ningún sitio entre la escala electrodébil y la escala de Planck, muy aburrido.

Pero el problema es mucho peor que eso.  El problema viene de nuestro amigo el Higgs.  Resulta que el Higgs es un campo con un bosón asociado, la partícula que está todo el mundo buscando como loco, el famoso y nunca hallado Bosón de Higgs.  Y claro, don bosón de Higgs tiene una masa (técnicamente estamos hablando del valor esperado del campo de Higgs en el vacío, pero masa está bien) y esa masa no puede estar (por límites experimentales) por encima de los 300 GeV (de hecho, alrededor de 250 GeV).

Tampoco pasa nada, pero sí… sí que pasa.  Como hemos dicho los parámetros de una teoría por debajo de una escala ha de tener relación con los parámetros de la teoría en el ultravioleta.

Así que, tenemos la masa del Higgs que está cómodamente en la escala electrodébil.  Pero resulta que cuando uno estudia las relaciones entre la masa del Higgs y la escala de Planck se lleva una sorpresa, y muy desagradable.  Si uno acepta que entre la escala electrodébil y la de Planck no hay nada (el desierto físico), entonces la relación entre la masa del Higgs y la escala de Planck lo obliga literalmente a crecer 17 ordenes de magnitud.  Es decir, que el Higgs debería de pesar la masa de Planck.  Pero si eso fuera así, entonces el mecanismo para el cual el Higgs es bueno que es dar masa a las partículas, no serviría.

Y ya para rematar, entra en juego la naturaleza y nos dice que la masa del Higgs no es del orden de la masa de Planck, sino que es del orden de la escala electrodébil (ya hemos dicho 250 GeV approx.)

Entonces, el problema está claro…  ¿Por qué el Higgs es ligero cuando debería de ser muy muy pesado?

Y aquí lo dejamos, este es el problema de la jerarquía.