domingo, 25 de agosto de 2013

Schwinger, ¿de dónde salen estas partículas? (30075)

Julian Schwinger

Aquí hemos hablado de las diferentes sorpresas a las que nos tiene acostumbrados la naturaleza a niveles cuánticos. 
 En esta ocasión no vamos a ser menos y nos vamos a enfrentar a un maravilloso efecto descrito por el físicos Julian Schwinger. 
 Es de recibo en este punto decir que este efecto fue anticipado por Sauter y posteriormente estudiado por Heisenberg y Euler.
Este efecto, como tantos otros, algunos de los cuales ya los hemos tratado aquí, se basa en las características del vacío cuántico. 
Como vamos a ver, el efecto consiste en la aparición de pares de partícula/antipartícula (fundamentalmente electrón-positrón) desde el mismo vacío por la presencia de un campo eléctrico de alta intensidad.

Los ingredientes fundamentales


Para visualizar este efecto necesitamos una serie de ingredientes bien sencillos. Hagamos una lista:
  1. Necesitamos un par de placas metálicas.
  2. Necesitamos conectar este par de placas a una pila.
(Evidentemente, las verificaciones experimentales de este efecto son un poco más complicadas, pero aquí únicamente quiero poner de manifiesto los ingredientes físicos relevantes, los detalles técnicos se los dejaremos a los experimentales )
Con este simple dispositivo conseguimos tener un campo eléctrico uniforme entre las placas, no hemos más que diseñado un condensador eléctrico:
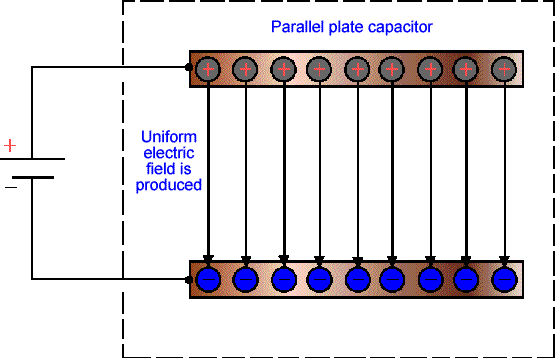
El valor del campo eléctrico entre las placas del condensador dependerá de la diferencia de potencial aplicada entre las placas y de la distancia entre las mismas.  
Asumiremos a partir de ahora que tenemos un vacío perfecto entre las placas.

¿Qué pasa con el vacío?


En teoría cuántica el vacío no puede ser un estado perpetuamente ‘tranquilo‘.
 Para que la teoría sea consistente, y se respete el principio de indeterminación, el vacío cuántico tiene que sufrir fluctuaciones. 

¿Esto qué quiere decir?

En cuántica el vacío se identifica como el estado de menor energía. Generalmente podemos decir que es el estado de energía nula (en un contexto no gravitatorio esto siempre es posible). 
Sin embargo, Heisenberg, a través de su principio de indeterminación obliga a que este estado no tenga una energía perfectamente determinada en todo instante de tiempo. 
El sistema en su estado de vacío puede tener fluctuaciones de energía 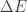\Delta E siempre y cuando su existencia tenga un tiempo de vida 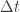\Delta t menor que el necesario para medirla, de forma que el producto de indeterminaciones verifique 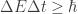\Delta E \Delta t\geq \hbar, donde 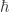\hbar es la constante reducida de Planck. 
De este modo, el estado de vacío tiene una energía en promedio nula pero instantáneamente está indeterminada. 
En algunas circunstancias podemos decir que estas fluctuaciones son análogas a la aparición de pares de partícula/antipartícula ‘virtuales‘ que son emitidas y absorbidas en un tiempo muy breve, tanto menor como mayor sea la energía empleada para crear el par desde el vacío. 
La imagen pictórica de este hecho es la siguiente:
En términos de los famosos diagramas de Feynman, lo que tenemos es que el sistema está en un estado vacío, y sin la participación de otras partículas aparece un par desde el vacío que vuelve a ser reabsorbido en el vacío:
¿Qué pasa si tengo un campo eléctrico?
Si tenemos un estado de vacío entre las placas de un condensador, el campo eléctrico interactuará con estos pares. Los positrones tendrán la tendencia de ir hacia la placa negativa y los electrones hacia la placa positiva.
Si el campo eléctrico es lo suficientemente intenso será capaz de impedir que el par se reabsorba en el vacío y las partículas pasaran a existir:
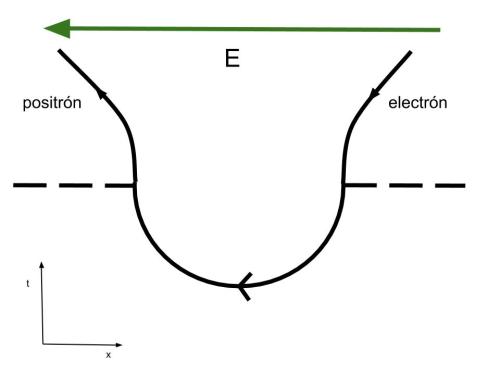
El campo eléctrico puede provocar, si tiene la suficiente intensidad, que el par 'virutal' pase a la existencia.
El campo eléctrico puede provocar, si tiene la suficiente intensidad, que el par ‘virutal’ pase a la existencia.
 Pero las partículas virtuales no son observables, en cierto sentido no son ‘reales‘, ¿cómo pasan a la existencia?
Lo que hace el campo eléctrico es ‘pagar’ la energía al vacío para que dichas partículas generadas del mismo adquieran masa y pasen a existir.
 Por lo tanto, el campo eléctrico en juego tiene que tener al menos tanta energía como 2\times m_{e}c^2.  
Es decir, que su intensidad ha de ser lo suficientemente alta como para poder generar dos partículas con la masa en reposo del electrón sin violar la conservación de la energía.
Literalmente, estas partículas nacen del vacío, pero no hay nada gratis en este universo, así que la energía para que este efecto tenga lugar ha de ser provista por un campo externo, en este caso el campo eléctrico.  
La probabilidad de que se de este efecto va con un factor:
P(Schwinger)\propto Exp\left[-\pi\dfrac{m^2}{qE}\right]
Esto implica que a mayor masa de las partículas que queramos crear menor probabilidad y a mayor campo eléctrico mayor probabilidad. 
Hay ciertas sutilidades en este proceso que lo hacen muy interesante. 
Es un efecto no lineal, no perturbativo, involucra al vacío cuántico y se estudia en el contexto de tiempo imaginario. 
Seguro que volvemos a este efecto para profundizar más adelante y para hablar de sus realizaciones experimentales con láseres de gran potencia, entre otras posibilidades.
Nos seguimos leyendo…
Publicado por en