Para los expertos en Kaluza-Klein y supergravedad cambiar de tópico de trabajo a la teoría de supercuerdas prometía muchos más éxitos.
Por todo ello creo que fueron abandonadas estas ideas. Como sus problemas aún no han sido resueltos y se cree que no tienen una solución elegante, siguen abandonadas. Permíteme recordar la situación de las teorías de Kaluza-Klein y de supergravedad antes del verano de 1984 (me basaré, como no, en M.J. Duff, B.E.W. Nilsson, C.N. Pope, “Kaluza-Klein Supergravity,” Physics Reports 130: 1-142, 1986, y en M.J. Duff, “Supergravity, Kaluza-Klein and superstrings,” pp. 18-60 en 11th Intl. Conf. General Relativity and Gravitation, Cambridge UP, 1987).
Los físicos creemos que la realidad está formada por dos entidades básicas: espaciotiempo curvado (la gravedad) y campos cuánticos (el modelo estándar).
Hay dos caminos posibles para una “teoría de todo” que unifique ambas entidades en la escala de Planck. El primero es que todo es espaciotiempo curvado y por tanto los campos (cuánticos) son el resultado de la existencia de dimensiones extra del espaciotiempo muy curvadas y de forma muy compacta. Copar con campos clásicos es fácil y esta es la idea de las teorías de Kaluza-Klein y de la supergravedad; sin embago, en el caso cuántico hay un grave problema, esta teoría no es renormalizable, como tampoco lo es la versión cuántica de la gravedad de Einstein, y por tanto no puede ser válida en la escala de Planck.
Y el segundo camino es que todo son campos cuánticos y el espaciotiempo es una entidad emergente, aunque por el momento no tenemos muy claro cómo emerge. Hay muchas propuestas en diferentes grados de desarrollo. La más popular y la que presenta un mayor grado de evolución es la asociada a campos cuánticos “cuerdísticos” (la generalización de los campos de partículas “puntuales” a campos de cuerdas y branas), en la llamada teoría de cuerdas y teoría M (ST/MT). Gracias a la simetría del espejo (“mirror symmetry”) y a la dualidad T se sabe que en esta teoría no existen las distancias menores que la longitud de Planck, aunque la descripción detallada de la teoría a esta escala no es conocida en detalle.
Sin embargo, hay muchas otras ideas para entender la emergencia del espaciotiempo; sin ser exhaustivo me vienen a la cabeza las siguientes posibilidades (todas en un grado de desarrollo que podemos calificar como “pobre” comparado con ST/MT y cuya consistencia interna está sujera a grandes dificultades técnicas aún no resueltas): las ideas asociadas a la gravedad cuántica de bucles (LQG), las ideas asociadas al principio holográfico, las asociadas a la causalidad de las interacciones entre campos como la teoría de triangulaciones dinámicas causales (CDT), y las asociadas a fuerzas entrópicas entre los campos como en la teoría de la gravedad entrópica de Erik Verlinde.
Para evitar malentendidos, me gustaría recalcar que la única teoría de gravedad cuántica consistente hasta el momento es la ST/MT y que en la actualidad hay físicos tratando de incorporar las demás ideas en el marco ST/MT con objeto de transformarlas en teorías consistentes.
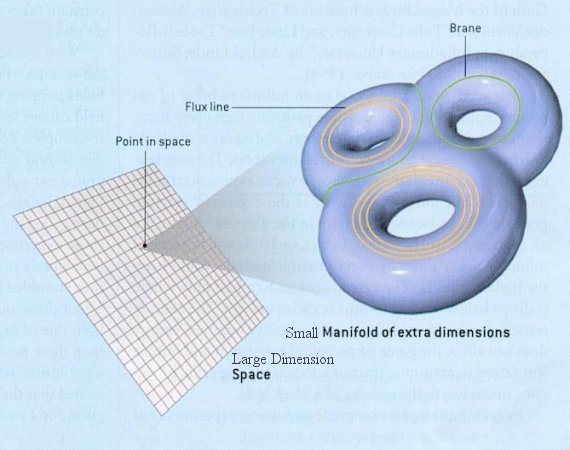
Volvamos a la idea de Kaluza-Klein, impecable a nivel clásico. Las ecuaciones de la gravedad de Einstein para un espaciotiempo con D>4 dimensiones describen además del gravitón (partícula de espín 2), bosones gauge (partículas de espín 1 descritas por ecuaciones de Yang-Mills) y bosones escalares llamados dilatones (de espín cero que se puede hacer que actúen como bosones de Higgs). La topología de las D – 4 dimensiones extra es diferente del resto, son compactas (cerradas y acotadas, como una esfera o un toroide), por lo que tienen un tamaño finito.
Las simetrías del modelo estándar, SU(3)xSU(2)xU(1), se pueden incorporar tomando un grupo G de simetría que contenga a SU(3)xSU(2)xU(1) y compactificando las dimensiones extra con una variedad diferenciable cuyo grupo de isometría sea G (a este idea se le suele llamar graviGUT, porque el grupo G define una teoría de gran unificación o GUT).
¿Por qué no observamos las D – 4 dimensiones extra del espaciotiempo?
En las teorías de Kaluza-Klein las cargas (gauge) son proporcionales a la constante de Newton de la gravedad y el factor es una función inversa al tamaño de las dimensiones extra; como las cargas gauge son muy grandes comparadas con la gravedad, recuerda que es muy débil, las dimensiones extra tienen un tamaño muy pequeño.
Lo habitual es tomar la escala de Planck (unos 10-33 cm). La versión cuántica de la teoría implica la existencia de nuevas partículas asociadas a campos confinados en las dimensiones extra campactas, llamadas partículas de Kaluza-Klein; no observamos estas partículas porque su masa es del orden de la energía de Planck (unos 1019 GeV).
Las teorías de Kaluza-Klein (o teorías graviGUT) tienen muchos problemas, pero mencionaré sólo tres de ellos. El primero es que la teoría no incorpora fermiones (leptones y quarks), que como en el caso del modelo estándar, han de ser introducidos ad hoc como en cualquier otra teoría GUT (luego no se trata de una teoría de todo, sino de “casi todo”).
El segundo es que la versión cuántica de estas teorías no es renormalizable (los problemas que aparecen al cuantizar la gravedad de Einstein en 4 dimensiones se mantienen en D dimensiones). Y el tercero que mencionaré es que la teoría no es quiral, a diferencia del modelo estándar, y no se conoce ningún mecanismo de rotura espontánea de la simetría que rompa una teoría no quiral en una teoría quiral. Que no me peguen los expertos.
Se han publicado soluciones a estas problemas, pero no son del todo satisfactorias. Por ejemplo, en lugar de usar las ecuaciones de Einstein para la gravedad que tienen derivadas hasta el segundo orden, como las ecuaciones de Newton, se puede usar una generalización con infinitas derivadas cuya versión cuántica parece ser renormalizable, pero que mantiene otros problemas.
Una solución natural para incorporar fermiones en una teoría de Kaluza-Klein es utilizar la supersimetría, que conduce a la teoría llamada supergravedad.
La supersimetría es una simetría que transforma fermiones en bosones y viceversa. Además, aplicar dos transformaciones supersimétricas equivale a una traslación en el espaciotiempo, es decir, la supersimetría equivale a una raíz cuadrada de una traslación (SUSY2=TRASLACIÓN). La supergravedad es la teoría tipo gauge basada en la supersimetría como simetría local y no hay que meter de forma explícita las ecuaciones de Einstein, ya que esta teoría incluye una partícula de espín 2, que actúa como gravitón, y la gravedad aparece de manera natural (algo parecido ocurre en QED al hacer la simetría U(1) local aparece el electromagnetismo como arte de magia). Asociado al gravitón hay partículas de espín 3/2 llamados gravitinos; su número es igual al número de supersimetrías diferentes de la teoría.
Hay varias razones teóricas en contra de la existencia de partículas de espín mayor de 2, por lo que el número máximo de supersimetrías es N=8. Este número de supersimetrías determina el espectro completo de partículas.
Por ejemplo, para N=8 supersimetrías hay un supermultiplete que contiene un gravitón (espín 2), 8 gravitinos (espín 3/2), 28 bosones vectoriales (espín 1), 56 fermiones de espín 1/2, y 70 bosones escalares (espín 0).
Una teoría de todo debe ser única (en algún sentido) y la supergravedad es única en D=11 dimensiones. La razón es que el número de supersimetrías impone un número máximo de dimensiones para el espaciotiempo.
Como el número de supersimetrías es N≤8 y un espinor de Dirac en 4 dimensiones tiene 4 componentes, el número máximo de componentes permitido para un espinor de Dirac en D dimensiones debe ser 32 lo que obliga a que D≤11 (el número de componentes de un espinor de Dirac es igual a 2(D-1)/2para D impar y 2D/2 para D par).
El espaciotiempo tiene 4 dimensiones, luego la teoría en 11 dimensiones debe tener 7 dimensiones extra compactificadas en el sentido de las teorías de Kaluza-Klein.
La dualidad entre supergravedades (N=1 en D=11)↔(N=8 en D=4) es muy sugerente y llevó a prestar mucha atención a la (única) teoría de la supergravedad N=1 en D=11 dimensiones. La gravedad en esta teoría descrita por un tensor métrico de 44 grados de libertad (componentes del campo del gravitón) y un gravitino de 128 componentes. La supersimetría obliga a que aparezcan campos bosónicos de 84 componentes (84+44=128). Además de aparecer las ecuaciones de Einstein sin ser impuestas, también surge la separación de las dimensiones extra M11=M4xM7, cuando el tensor de cuatro índices de intensidad del campo gauge de 84 componentes es constante (es decir, lo más simple posible)
. La fenomenología de la teoría N=8 en D=4 da muchos problemas y es preferible una teoría N=1 en D=4; a principios de los 1980 hubo mucho revuelo cuando se descubrió que tomando M7=S7 (la esfera en 7 dimensiones) aparece de forma natural un mecanismo de Higgs que rompe la supersimetría N=8 en D=4 en la supersimetría N=1 en D=4, pero su grupo de holonomía H(M7)=G2 que implica un grupo gauge SO(8) que no es suficiente para contener el modelo estándar SU(3)xSU(2)xU(1). Hay otras propuestas para M7 que permiten grupos más grandes capaces de albergar el modelo estándar, pero ninguna admite una rotura de simetría “natural” hasta N=1.
Volvamos al principio, ¿por qué se abandonó la idea de la supergravedad N=1 en D=11 tras el verano de 1984 cuando en 1983 podríamos decir que había euforia por ella?
Como es obvio influyó la primera revolución de la teoría de cuerdas, la teoría de supercuerdas de 1984, pero hay razones más importantes que están descritas en todos los artículos de revisión sobre esta teoría. Destacaré tres de ellas.
La primera es un artículo de Edward Witten que mostró que una supergravedad en D=11 con dimensiones extra compactificadas en una variedad diferenciable no puede ser rota de forma espontánea a una teoría quiral en D=4 dimensiones. Si la teoría no es quiral en D=11 entonces tampoco lo puede ser en D=4 (la quiralidad se preserva en dimensiones impares y sólo puede surgir en la rotura de simetría en espaciotiempos con dimensión par). Para resolver este problema se puede “complicar” la teoría en D=11 introduciendo ad hoc la quiralidad o usando simetrías “ocultas”, pero la unicidad, la simplicidad y la belleza de la teoría desaparece.
Los pocos expertos que siguieron investigando en supergravedad tras la revolución de la teoría de cuerdas se concentraron en la teoría en D=10 dimensiones. Pero los fermiones quirales tienen asociados la aparición de anomalías quirales que violan las simetrías gauge de la teoría Yang-Mills en D=4; se pensó que podrían ser eliminadas con una compactificación adecuada, pero se demostró en 1983 que dicha compactificación no existe.
Para resolver este problema basta compactificar en una variedad que no sea diferenciable (como una red discreta), pero a mucha gente no le gusta esta idea porque no se puede recuperar de forma fácil el modelo estándar.
La segunda razón por la que en 1985 se relegó a un segundo plano la idea de la supergravedad N=1 en D=11 fue que la compactificación de las dimensiones extra introduce una constante cosmológica enorme, proporcional a la masa de Planck al cuadrado; en aquel momento se pensaba que la constante cosmológica era nula (hoy sabemos que existe la energía oscura, pero la constante cosmológica es unos 120 órdenes de magnitud más pequeña que la masa de Planck al cuadrado). Hoy en día se pueden reducir estos 120 órdenes de magnitud a menos de 60 (según los detalles técnicos), un número que sigue siendo enorme.
La tercera razón, quizás la más importante es que la teoría no es renormalizable y presenta divergencias ultravioletas.
Ha habido progresos recientes en la renormalización de “la supergravedad N=8” (yo los califiqué en este blog de forma muy optimista como “una nueva revolución en la física teórica“), pero el problema de fondo sigue siendo el mismo. Aunque la teoría sea renormalizable hasta 5 bucles, hay argumentos fuertes en contra a partir de 7 bucles, inclusive.
Hoy en día no parece que la teoría pueda ser renormalizable a todos los órdenes.
La teoría de cuerdas, por el contrario, parece finita a todos los órdenes.