alquimiayciencias: La constante de Euler-Mascheroni (29965)

En Matemáticas hay varias constantes, digamos, extrañas que son muy conocidas, como por ejemplo el número pi y el número e.

Quien más quien menos las conoce y ha trabajado con ellas.

Pero también hay constantes interesantes que no son tan conocidas.

En este post vamos a hablar de una de ellas: la constante de Euler-Mascheroni, que se representa con la letra griega gamma: 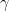$\displaystyle\gamma$ .

Esta constante se define de la siguiente forma:

$\mathbf{\displaystyle\gamma=\lim_{n \rightarrow \infty }\left( \sum_{k=1}^n \frac{1}{k}-\ln(n) \right)}$

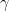Es decir, $\displaystyle\gamma$ se define como el límite de la diferencia de la sucesión de sumas parciales de la serie armónica y el logaritmo neperiano.

Otras formas de definirla son las siguientes:

$\displaystyle\gamma=\int_1^\infty\left({1\over\lfloor x\rfloor}-{1\over x}\right)\,dx=- \int_0^\infty { \ln(x) \over e^x }\,dx$

Su valor aproximado es: $\displaystyle\gamma \simeq 0,577\;215\;664\;901\;532\;860\;607\;\ldots$

No se sabe si 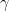$\displaystyle\gamma$ es un número racional.

Lo que sí se conoce es que si lo fuera su denominador sería

mayor que 10²⁴²⁰⁸⁰.

Casi nada.

En diciembre del año 2006 Alexander J. Yee calculó la constante de Euler-Mascheroni con más de 116 millones de cifras decimales, récord para este número.

Vamos a ver algunas expresiones más en las que aparece 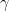$\displaystyle\gamma$ :

Integrales cuyo resultado es 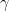$\displaystyle\gamma$

$\displaystyle\gamma=-\int_0^1 { \log\log\left (\frac{1}{x}\right ) }\,dx$ $\displaystyle\gamma= \int_0^\infty { \frac{1}{x} \left ( \frac{1}{1+x}-e^{-x} \right ) }\,dx$

Integrales que involucran a 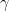$\displaystyle\gamma$

$\displaystyle\int_0^\infty { e^{-x^2} \log x }\,dx = -\tfrac14(\gamma+2 \log 2) \sqrt{\pi}$

$\displaystyle\int_0^\infty { e^{-x} \log^2 x }\,dx = \gamma^2 + \frac{\pi^2}{6}$ (¿les suena ese $\displaystyle\frac{\pi^2}{6}$ ?)

Relación con $\displaystyle \log{\frac{4}{\pi}}$

$\displaystyle\gamma = \int_{0}^{1}\int_{0}^{1} \frac{x-1}{(1-x\,y)\log(x\,y)} \, dx\,dy = \sum_{n=1}^\infty \left ( \frac{1}{n}-\log\frac{n+1}{n} \right )$

$\displaystyle log \left ( \frac{4}{\pi} \right ) = \int_{0}^{1}\int_{0}^{1} \frac{x-1}{(1+x\,y)\log(x\,y)} \, dx\,dy = \sum_{n=1}^\infty (-1)^{n-1} \left( \frac{1}{n}-\log\frac{n+1}{n} \right)$

Relación con la función $\displaystyle\Gamma$

$\displaystyle\gamma = \lim_{n \to \infty} \left [ \frac{ \Gamma(\frac{1}{n}) \Gamma(n+1)\, n^{1+1/n}}{\Gamma(2+n+\frac{1}{n})} - \frac{n^2}{n+1} \right ]$