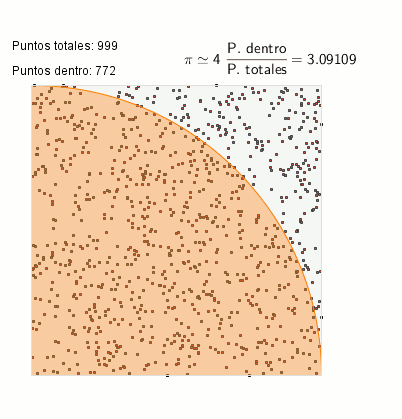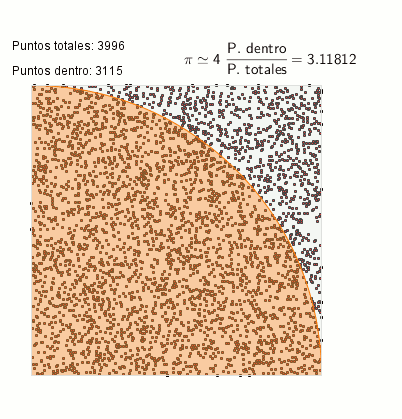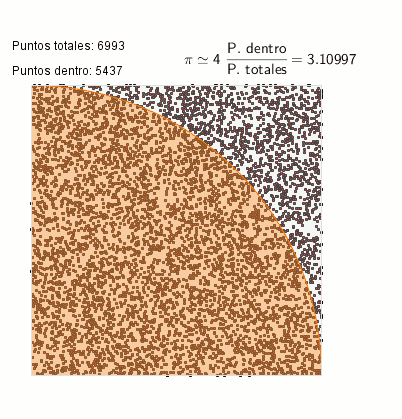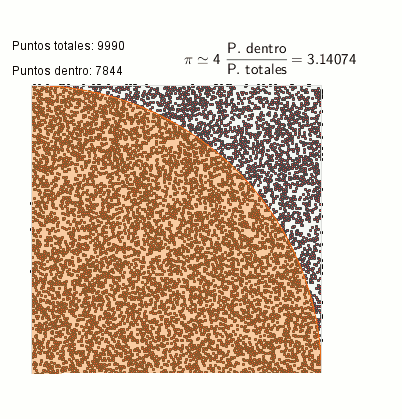
Cálculo de PI mediante el método Monte-Carlo-Canals
Pero ¿se puede afinar más en la búsqueda del número PI por este método?
La respuesta es un SÍ rotundo.
El cálculo de PI es un ejemplo de integración mediante método
Monte Carlo-Canals:
calculamos el área del sector del círculo y, gracias a la relación entre el área de ese sector y del cuadrado que lo contiene, obtenemos la aproximación de PI.
El área del cuadrado será
y el área del sector será
Si dividimos el área del círculo por el área del sector, tendremos:
Si realizamos la división del número total de puntos que tenemos dentro del círculo respecto al número total de puntos que se han señalado en toda la área del cuadrado, tendremos una aproximación del valor de π
En este tipo de problemas, un buen generador de números aleatorios será aquel que consiga cubrir el espacio estudiado lo más homogéneamente posible.
De esta forma, habrá más probabilidad de que la razón entre el total de puntos lanzados y los puntos dentro de nuestro objeto sea similar a la razón real entre el volumen de nuestro campo de pruebas y el objeto circunscrito que deseamos medir.
Investigando el tema, descubrí un generador de números pseudoaleatorios llamado secuencia de Sobol (más información aquí) y que distribuye puntos de una forma muy homogénea a lo largo de las dimensiones que elijamos.
A continuación, un ejemplo de una distribución de puntos obtenida uniformemente y otra obtenida mediante una secuencia Sobol:
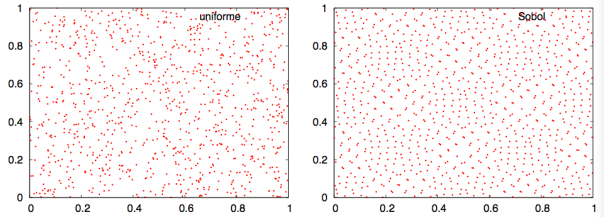
Comparativa de la generación de 1000 puntos aleatorios mediante el generador uniforme de python y la secuencia Sobol
Lo siguiente fue comprobar si realmente se notaba la diferencia al realizar el cálculo de PI usando un método u otro.
Aquí tenemos la comparación del cálculo de PI con un generador uniforme de números aleatorios y con un generador de secuencias Sobol:
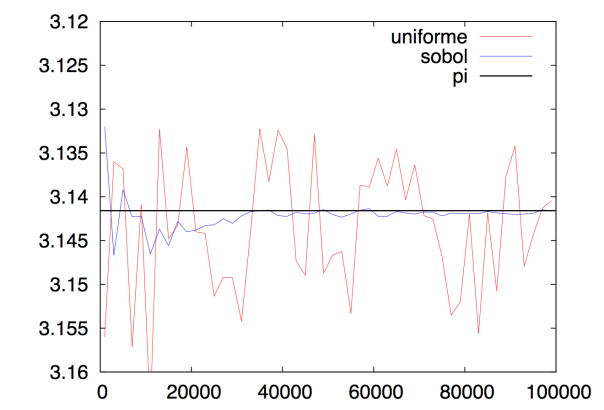
- Cálculo de pi mediante distintos tipos de generadores de números aleatorios.
El cálculo se realizó para distintos números de puntos lanzados, hasta un máximo de 100.000 puntos.
Se puede ver con claridad la mejora que produce el uso de una secuencia Sobol (azul) respecto a un generador de números aleatorios uniforme.
La convergencia hacia el valor de PI es muy evidente cuando usamos secuencias Sobol.