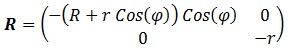El donut (matemáticamente conocido como toro o toroide) es una superficie cerrada (es decir, encierra un volumen) que reside en el espacio 3-dimensional, por lo que para analizarlo sólo será necesario conocer la teoría de superficies elemental.
Ecuación Implícita del Donut:
La ecuación implícita de una superficie, recordemos, es aquélla que está igualada a “0″, y que todos los puntos de la misma la cumplen.
Si suponemos que nuestro donut está centrado en el origen de coordenadas sobre el plano horizontal, es obvio que esta ecuación tendrá una simetría de rotación respecto al eje “z”, es decir, que en todo momento “x^2 + y^2″ van a aparecer juntos. Si cuando acabemos ésto no sucede, podemos asegurarnos de que vamos mal.
En primer lugar, nuestro donut se puede interpretar como una circunferencia de radio “R” con un grosor “r”, es decir, los puntos de la circunferencia base “c” de nuestra superficie será:
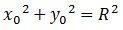
Ahora, sabemos que los puntos “P” de nuestro donut tienen que poseer una distancia mínima “r” a la circunferencia base, cálculo para el que tambien podemos trabajar con el cuadrado de dicha distancia:
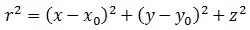
Dejando “y0″ en función de “x0″:
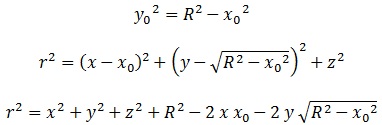
podemos derivar respecto a “x0″ para garantizar el mínimo de “r” si la derivada es igual a 0.
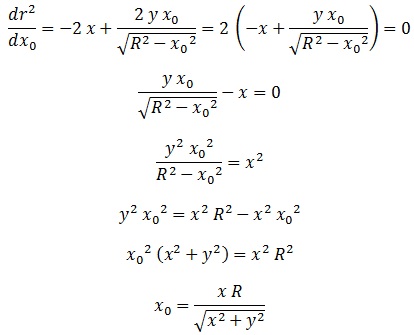
Ahora, si retomamos la ecuación que teníamos llegamos a:
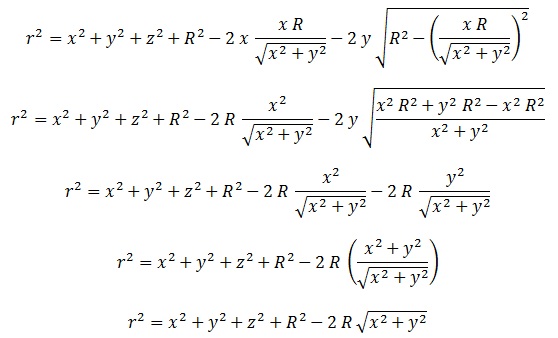
, que nos da la ecuación implícita de nuestra superficie del toro:
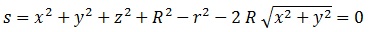
Si nos fijamos, vemos que tal y cómo supusimos que iba a pasar, las “x” y las “y” aparecen siempre juntas como una suma de cuadrados debido a la simetría de rotación sobre “z”.
Parametrización del Donut:
Una parametrización matemática “s” de una superficie se decía matemática si para llegar a ella hacíamos cuentas a partir de su ecuación “s”.
Para parametrizar matemáticamente la ecuación a la que hemos llegado tendremos que aplicar siempre trigonometría, y empezaremos devolviendo “r^2″ a la derecha de la ecuación para después divirirla toda entre él.

Parametrizaremos inicialmente según el ángulo “φ”:
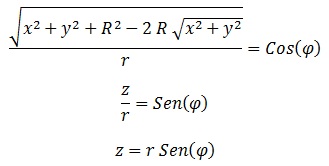
De aquí obtenemos:
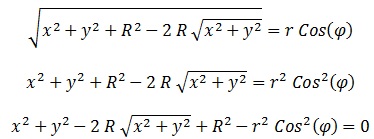
Resolviendo “(x^2 + y^2)^(1/2)” como si fuese una ecuación de segundo grado:
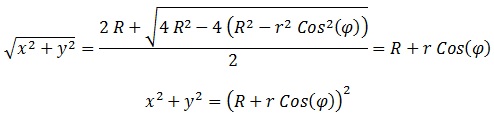
Y procedemos a parametrizar con un nuevo ángulo “σ”:
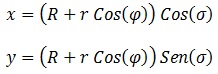
aplicando trigonometría, como hemos hecho en casi todas las parametrizaciones de superficies .
En conclusión, nuestro donut parametrizado será:
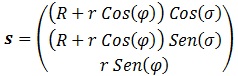
La cual, personalmente, yo calificaría de intuitiva porque es fácil llegar a ella sin hacer cuentas, teniendo en cuenta que el valor de “z”, la altura, viene dado por el grosor “r” de la circunferencia base proyectado con el ángulo de elevación “φ”, mientras que “x” e “y” definen una circunferencia de radio “R” más la proyección horizontal del grosor.
Es muy importante tener en cuenta que si:
- r > R.
el donut pierde el agujero y se corta a sí mismo, por lo que dejamos de estar ante una parametrización regular.
1ª Forma Fundamental del Donut:
Recordemos que la 1ª forma fundamental “g” era una matriz definida con las derivadas parciales del modo:
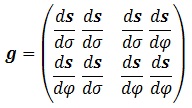
, por lo que necesitamos las derivadas parciales del donut en este proceso, así como sus productos escalares:
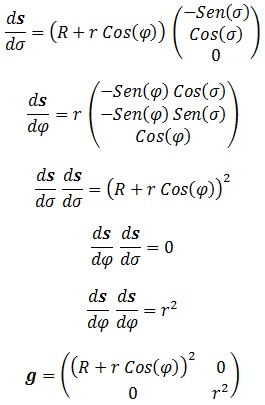
Área del Donut:
Ahora, recordando el área de una superficie definida mediante su parametrización, obtenemos:
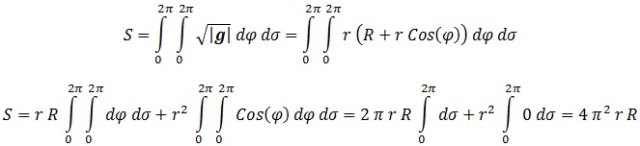
Vector Normal al Donut:
El vector normal a una superficie, recordemos, se definía como el vector unitario en la dirección del gradiente de la ecuación implícita:
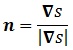
Así que tenemos que obtener el gradiente del donut:
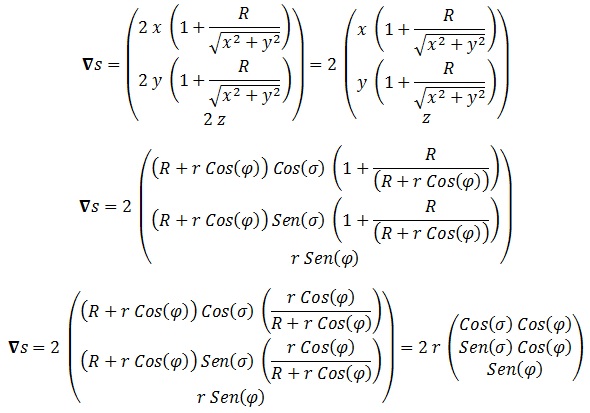
En resumen:

2ª Forma Fundamental del Donut:
La segunda forma fundamental era la matriz definida como:
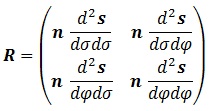
, es decir, en esta ocasión necesitamos conocer las derivadas segundas:
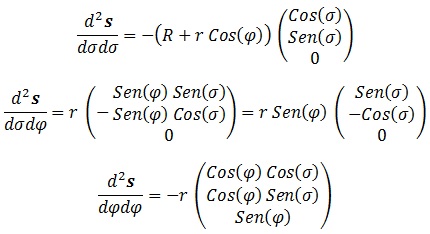
, y los coeficientes de “R” son:
Curvatura del Donut:
La curvatura de una superficie se definía como el determinante de la 2ª forma fundamental, de modo que la curvatura de nuestro donut es:
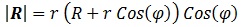
Y, por primera vez, nos topamos con una figura cuyo signo de la cruvatura depende de un parámetro, a saber, “φ”. Analicemos un poco más detenidamente esta propiedad, que hace a nuestro donut tan interesante matemáticamente hablando.
.-φ toma valores [0, π/2) ó (3π/2, 2π):
En este caso el coseno es positivo y la curvatura también, debido a que si colocamos un plano sobre cualquiera de ellos de un modo tangente, ¡tan solo tocaremos al punto en cuestión!, y además todo el donut quedará al mismo lado del plano.
.-φ toma valores (π/2,3π/2):
En este caso el coseno es negativo y la curvatura también. Nos encontramos en la parte interior del donut, la que forma el agujero. ¡Es imposible tocar cualquiera de nuestros puntos con un plano firme sin cortar el donut en 2 pedazos!
.-φ toma valores “π/2″ ó “3π/2″:
En este caso el coseno y la curvatura son nulos. Ésto se debe a que nos encontramos o bien en la parte superior o bien en la parte inferior del donut, y si colocamos un plano tangente sobre estos puntos es seguro que contendrá a la circunferencia superior (o inferior, según el caso) del mismo.
Como ni todo el donut está al mismo lado del plano (hay curvas sobre él), ni es cortado por éste, la curvatura no puede ser positiva ni negativa, y nos resulta neutra.