Tras haber visto la Teoría de Curvas vamos a dar un salto de una dimensión en nuestro punto de vista hacia las superficies, que constituyen un elemento imprescindible en grandes teorías físicas, dados los conceptos a los que tendremos que recurrir para estudiarlas.
Definición Matemática de una Superficie:
Si bien decíamos que las curvas eran objetos matemáticos con un grado de libertad, las superficies serán objetos de matemáticos con 2 grados de libertad, por lo que tendremos que recurrir a dos parámetros libres si la definimos con una parametrización de la forma “s(u, v)“.
Una vez más, haciendo referencia a la otra forma de definir una superficie, que es mediante ecuaciones, implica “N-2″ de las mismas, siendo “N” la dimension de nuestro espacio. O dicho de otra forma, si queremos definir una superficie mediante una única ecuación debemos ubicarnos en el 3-espacio euclídeo, porque de otro modo necesitaremos más o menos.
Visualmente, si la curva la interpretábamos como la trayectoria que seguía una partícula a lo largo del tiempo, la superficie podemos interpretarla como el conjunto de rutas limitadas por el entorno que puede seguir una partícula en el espacio o la trayectoria del movimiento de una curva.
Más adelante veremos más claros éstos conceptos.
Tipos de Parametrización:
De nuevo, como sucedía con las curvas, podemos calificar las parametrizaciones como intuitivas, matemáticas o sobre coordenadas, siendo excluyentes tan solo el primer y el segundo método. Probemos con algunos ejemplos de cada:
.-Parametrización Intuitiva:
El mejor ejemplo de parametrización intuitiva de una superficie es la que podríamos tener del plano. Si consideramos a nuestro plano como una recta:
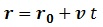
, simplemente tenemos que sumar una segunda traslación a nuestra inicial “v t”, de modo que:
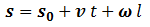
Podemos considerar también intuitiva la parametrización de las superficies cuádricas degeneradas vistas en geometría en el espacio, como es el caso del cilindro:

, pues, en analogía con la circunferencia, observamos:
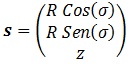
, parametrización que además coincide con las coordenadas cilíndricas vistas en geometría espacial también. Si nos fijamos, las componentes “sx” y “sy” definen una circunferencia en función del parámetro “σ”, y ésta circunferencia está a una u otra altura según el valor de “z”.
Así construimos perfectamente un cilindro circular sin problema.
.-Parametrización Matemática:
La parametrización matemática será (he de decir que lamentablemente) la más común entre las superficies, pues es la forma más correcta de ver los parámetros de la mayoría de ellas.
Veamos las parametrizaciones de algunas superficies cuádricas tales como el cono, la esfera, el hiperboloide de 1 hoja o el paraboloide hiperbólico.
Cono:
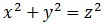
La forma usual de proceder ante esta ecuación sería buscar analogías, como siempre, con la trigonometría, de modo que:
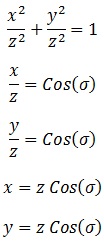
Finalmente, nuestro cono quedaría parametrizado según “σ” y “z”:

Si buscamos analogías con el cilindro, podemos apreciar que, en realidad, ésta debería considerarse una parametrización intuitiva, pues seguimos trasladando circunferencias a lo largo de “z”, con la única diferencia de que en este caso el radio de cada una depende de “z” también.
..-Esfera:

Parametrizaremos de golpe toda la esfera, buscando, como siempre, razones trigonométricas:
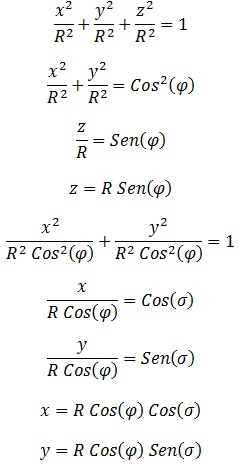

En este caso tenemos parametrizada nuestra esfera (con plano de ecuador en “z=0″) según nuestro ángulo “σ”, idéntico a los casos anteriores, y el ángulo de elevación “φ”, que apreciemos, no está expresado en coordenadas esféricas, pues indica la inclinación con respecto al ecuador y no con respecto al polo.
Podemos interpretar esta parametrización como un conjunto de circunferencias horizontales que, a medida que se alejan del ecuador, se achatan siguiendo también un arco de circunferencia.
Hay muchas otras formas frecuentes de parametrizar la esfera, pero ahora no nos ocupan.
..-Hiperboloide de 1 Hoja:
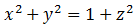
En esta ocasión recurriremos a la trigonometría hiperbólica para parametrizar:
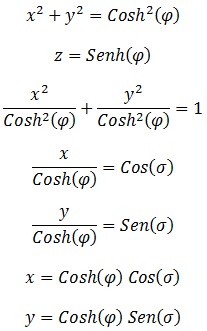

Esta parametrización es un tanto más difícil de interpretar, pero el radio de nuestras circunferencias aumentaria simétricamente con la distancia al origen siguiendo una hipérbola.
Los hiperboloides tendrán una importancia crucial en los Espacios de Minkowski donde se asienta toda la Teoría General de la Relatividad, los cuales explicaré dentro de unas cuantas entradas.
.-Parametrización Sobre Coordenadas:
Consideremos ahora el paraboloide hiperbólico que gira “π / 4″ radianes las componentes “x” e “y” del anterior según la transformación de los ángulos de Euler:
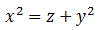
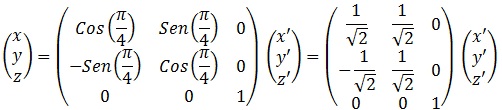
, obtenemos:
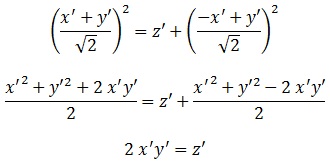
Parametrizar este paraboloide ahora según “x” e “y” es tan simple como:
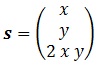
Y además es muy fácil de interpretar geométricamente, puesto que todo el rato la altura de un punto para unos valores dados “x” e “y” no es ni más ni menos que el doble del producto de ambos.
Además, si “x” o “y” son negativos la superficie irá hacia abajo, si alguno de ellos son nulos la altura será 0, y si ambos poseen el mismo valor absoluto (planos trasversales a 45º entre los ejes x-y) la superficie tomará la forma de parábolas hacia arriba o hacia abajo, lo que quiere decir que en los cuadrantes del plano horizontal opuestos “z” posee el mismo signo, y que existen dos planos verticales que pasan por el origen, a los cuales la superficie corta con líneas rectas, y otros dos a los que corta con parábolas.
Curvas Singulares:
Procedemos ahora a analizar algo que llevamos haciendo todo el rato, y es ver qué pasa cuando analizamos un único parámetro de la superficie, haciendo el otro constante.
Se define como curva singular de la parametrización a la curva que resulta de hacer alguno de los dos parámetros libres “u”, “v” constantes, y como curva singular genérica a la que resulta de dejar uno de los parámetros en función del otro (incluyendo el caso en que es constante).
Ejemplos de curvas singulares de la parametrización han sido todas las circunferencias de las que hablamos anteriormente, y en el caso del paraboloide hiperbólico las rectas y las parábolas.
Un ejemplo de curva general genérica sería, por ejemplo en nuestro cilindro, suponer:

, de modo que la parametrización resultaría:

¡Nada más ni nada menos que una hélice circular!
Aquí tenemos, pues, un ejemplo de curva singular del cilindro no propia de la parametrización.
De ahora en adelante, dada una superficie “s(u, v)“, denominaré “su” a la curva singular que hace constante “v” y “sv” a la curva que hace constante “u”.
Dichas curvas representan dos posibles trayectorias que puede seguir un punto cualquiera de la superficie sobre ella, y de cada una ellas, lógicamente, podemos analizar la longitud, curvatura y torsión, así como el triedro móvil. Pero lo que nos va a interesar ahora es saber el ángulo que forman entre ellas.
Ángulo Entre Dos Curvas Singulares de la Parametrización:
Vamos a proseguir ahora considerando lo que sabíamos de curvas sobre vectores tangentes a las mismas, es decir, que se obtienen derivando una vez respecto a la variable pertinente.
Así pues, los vectores “velocidad” o “dirección” de nuestras curvas se definen, respectivamente como:

El producto escalar de estos vectores se define como:

, donde “α” representa el ángulo entre ambos vectores, es decir ¡el ángulo entre la dirección de ambas curvas! Ya podemos calcular lo que queríamos:
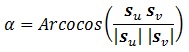
Plano Tangente:
Conocidos nuestros dos vectores “su” y “sv” en un punto “s0” de la superficie es posible definir el plano tangente a la superficie en ese punto “s0” como el plano de la forma:
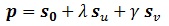
, que al seguir la dirección de dos vectores tangentes tiene que serlo también a la fuerza. El plano tangente nos será muy útil a la hora de tratar con la curvatura, pues da una idea geométrica útil para su interpretación.
Vector Normal:
Si nuestra superficie vive en un 3-espacio podemos, además, definir ahora un vector perpendicular a la superficie punto a punto, “n(u, v)“, aplicando una norma que conocemos muy bien, y es que el vector perpendicular al plano tangente es perpendicular a sus vectores directores, de modo que sólo tenemos que realizar un producto vectorial entre ambos para garantizarlo.
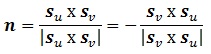
El único problema que tiene esta definición es elegir cuál es la curva que va primero en el producto vectorial, puesto que de ello depende el sentido del vector normal. Si la curva es cerrada, es decir, contiene un volumen finito, lo general es considerar el sentido que vaya hacia fuera de la misma.
En cualquier otro caso, se recurre a la libre elección.
Veamos el caso de la esfera:
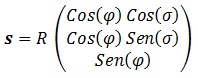
Tenemos las curvas con “φ”, “σ” constantes, cuyos vectores directores en cada punto son:

El ángulo entre ellos será:
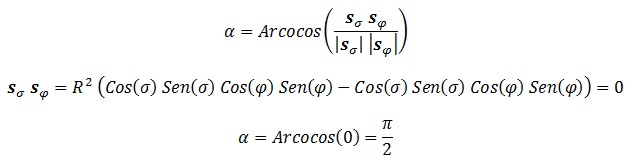
Es decir, son perfectamente perpendiculares, lo que nos garantiza que el vector normal no va a ser nulo. Veamos ahora qué pasa si hacemos cada uno de los distintos productos vectoriales:
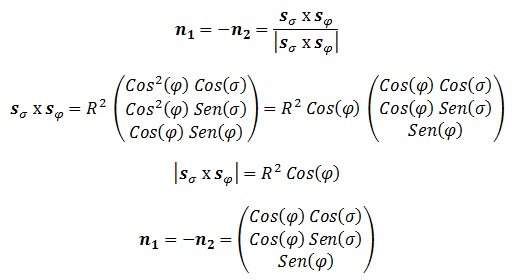
En este caso es obvio que el segundo vector se dirige hacia el centro de la esfera y el primero hacia fuera, por lo que el vector normal que usaremos por convenio será “n1“.
Otra forma de obtener el vector normal es usar el vector gradiente “D“:

Para ello, volveremos a nuestra ecuación de la esfera:
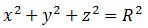
y la escribimos en forma implícita, es decir, igualada a “0″:
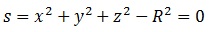
El vector normal se define (salvo por un signo) como:
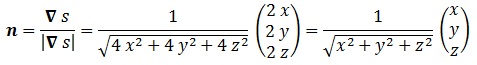
Aplicando ahora los cambios de la parametrización:
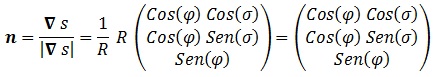
Resultado exactamente idéntico al que teníamos antes.
Parametrización Regular:
¿Qué hace que una parametrización sea respetable?
En el caso de las curvas nos llegaba con que fuese derivable en todo el dominio y que su módulo nunca fuese nulo.
En las superficies vamos a ser un poco más exigentes y vamos a pedir que sea 2-derivable con respecto a ambos parámetros, y que el vector normal no se anule en ningún momento, de aquí deducimos que las curvas singulares deben ser regulares, y además, no pueden ser paralelas en ningún momento. Una parametrización de superficie que cumpla con todos estos requisitos será considerada una buena parametrización.
1ª Forma Fundamental:
Existe una matriz g simétrica asociada a cada parametrización conocida como métrica, definida como:
- gij = s’i s’j.
En total, solo existen cuatro coeficientes, pues la matriz es 2 x 2.
En el caso de la esfera, tenemos:
- s’σ = (- R Cosφ Senσ, R Cosφ Cosσ, 0), φ = cte.
- s’φ = (- R Senφ Cosσ, – R Senφ Senσ, R Cosφ), σ = cte.
- gσσ = (s’σ)^2 = R^2 (Cosφ)^2.
- gσφ = gφσ = s’σ s’φ = 0.
- gφφ = (s’φ)^2 = R^2.
De modo que la matríz métrica de nuestra parametrización es:
- g = [R^2 (Cosφ)^2, 0; 0, R^2].
Elemento de Area:
Nuestra métrica va a tener la importante propiedad de definir el elemento de area de la forma:
- da = |g|^(1/2) du dv.
, de modo que el area de una region de nuestra superficie es:
- a = ∫|g|^(1/2) du dv.
Veamos por última vez en esta entrada qué sucede con nuestra esfera.
- |g| = R^4 (Cosφ)^2.
- |g|^(1/2) = R^2 Cosφ.
- a = ∫(∫R^2 Cosφ dσ desde “0″ hasta “2 π”) dφ desde “- π / 2″ hasta “π / 2″.
- a = R^2 ∫Cosφ (∫ dσ desde “0″ hasta “2 π”) dφ desde “- π / 2″ hasta “π / 2″.
- a = R^2 ∫Cosφ 2 π dφ desde “- π / 2″ hasta “π / 2″.
- a = 2 π R^2 ∫Cosφ dφ desde “- π / 2″ hasta “π / 2″.
- a = 2 π R^2 (2).
- a = 4 π R^2.
La superficie que todos conocíamos.
2ª Forma Fundamental:
Existe una segunda matriz 2 x 2 “ς” que cuya importancia no es menos relevante, y que se define como:
- ςij = s”ij n.
, donde “s”ij” representa la doble derivada, primero respecto a la variable “j”, y después respecto a la variable “i”:
- s”ij = d(ds / dj) / di.
Una vez más, deducimos que los cuatro coeficientes son:
- ςii = n d(ds / di) / di.
- ςij = ςji = n d(ds / dj) / di.
- ςjj = n d(ds / dj) / dj.
Veamos qué pasa en 3 casos:
.-Plano:
- s = z = 0.
La parametrización es libre para “x” e “y”, porque lo único que está fijado es el valor de “z”:
- s = (x, y, 0).
- n = D s / |D s| = (1, 1, 0) / 2^(1/2).
- d(ds / dx) / dx = (0, 0, 0).
- d(ds / dy) / dx = (0, 0, 0).
- d(ds / dy) / dy = (0, 0, 0).
- ςxx = 0.
- ςxy = ςyx = 0.
- ςyy = 0.
- ς = [0, 0; 0, 0].
.-Paraboloide Elíptico:
- s = x^2 + y^2 – z = 0.
Haciendo una parametrización sobre coordenadas:
- s = (x, y, x^2 + y^2).
- n = D s / |D s| = (2 x, 2 y, -1) / (4 x^2 + 4 y^2 + 1)^(1/2).
- d(ds / dx) / dx = (0, 0, 2).
- d(ds / dy) / dx = (0, 0, 0).
- d(ds / dy) / dy = (0, 0, 2).
- ςxx = – 2 / (4 x^2 + 4 y^2 + 1)^(1/2).
- ςxy = ςyx = 0.
- ςyy = – 2 / (4 x^2 + 4 y^2 + 1)^(1/2).
- ς = [- 2 / (4 x^2 + 4 y^2 + 1)^(1/2), 0; 0, - 2 / (4 x^2 + 4 y^2 + 1)^(1/2)].
.-Paraboloide Hiperbólico:
- s = x y – z = 0.
Este hiperboloide es parecido al que parametrizamos antes, así que por coordenadas recordamos que queda como:
- s = (x, y, x y).
- n = D s / |D s| = (y, x, -1) / (y^2 + x^2 + 1)^(1/2).
- d(ds / dx) / dx = (0, 0, 0).
- d(ds / dy) / dx = (0, 0, 1).
- d(ds / dy) / dy = (0, 0, 0).
- ςxx = 0.
- ςxy = ςyx = – 1 / (y^2 + x^2 + 1)^(1/2).
- ςyy = 0.
- ς = [0, - 1 / (y^2 + x^2 + 1)^(1/2); - 1 / (y^2 + x^2 + 1)^(1/2), 0].
Curvatura:
Ahora bien, ¿para qué nos ha servido calcular todo esto?
La curvatura de de cada punto de la superficie, definida como “|ς|” nos da una idea de la forma que tiene en todo momento, ¡y además nos servirá en entradas muy posteriores para medir la dilatación del tiempo relativista!
O dicho de otra forma, este término matemático es todo un regalo para los físicos.
Sobre la curvatura de superficies pondré muchos ejemplos posteriormente, pero por ahora veamos qué pasa con nuestras tres superficies anteriores. Las curvaturas del plano, el paraboloide hiperbólico y el paraboloide elíptico son, por orden:
- |ς| = 0.
- |ς| = 4 / (4 x^2 + 4 y^2 + 1).
- |ς| = – 1 / (y^2 + x^2 + 1).
En el primer caso, vemos que la curvatura del plano es “0″ en todo momento, lo cual es obvio dado que no se curva en ningún momento. Pero, ¿implica que la curvatura sea “0″ que nuestra superficie sea plana? ¡Para nada! Para que nuestra superficie sea plana la curvatura debe anularse, pero además todos los coeficientes de “ς” deben ser nulos.
Al conjunto de puntos de una superficie que anulan la curvatura se les denomina Puntos Parabólicos, y geométricamente se interpretan de modo que el plano tangente sobre los mismos contiene algún segmento recto de la superficie y todos los demás puntos están a un único lado de éste en las proximidades del lugar. Otro ejemplo de puntos con curvatura parabólica son los de un cilindro elíptico, pues los planos tangentes siempre contienenen a la recta directriz del mismo.
En el segundo caso la curvatura siempre es positiva, puesto que tenemos un número positivo dividido entre números positivos.
Los puntos con esta propiedad son denominados Puntos Elípticos, y cumplen que, en las proximidades a los mismos, toda la superficie está contenida a un lado del plano tangente. Ahora le vemos más lógica al hecho de que a esta figura se la denomine paraboloide elíptico.
Otro ejemplo típico de curvatura elíptica es la esfera, pues siempre está enteramente contenida a un único lado de cada uno de sus planos tangentes.
El hiperboloide de 2 hojas tiene curvatura elíptica por el mismo motivo, pero aquí la descripción del plano sólo nos sirve localmente: si consideramos el plano tangente a un punto de una de las hojas, ésta quedará a un lado del mismo, pero la otra en el lado opuesto, de ahí la importancia de especificar “en la proximidad del punto en cuestión”.
Por último, la curvatura de nuestro paraboloide hiperbólico es siempre negativa, y lógicamente a los puntos con esta propiedad se los denomina Puntos Hiperbólicos. Dado que los parabólicos contenían segmentos rectos de la curva y todos los demás puntos estaban a un lado y los elípticos dejaban a toda la superficie hacia un mismo lado, es obvio que los hiperbólicos son aquéllos que contienen fragmentos de superficie a ambos lados del plano tangente, es decir, se curvan en sentidos opuestos según la dirección. Otro buen ejemplo de curvatura negativa es el hiperboloide de 1 hoja.
Por supuesto, existen superficies con varios tipos de curvatura distintos, y un buen ejemplo de ello es el toroide (del cual hablaré en la próxima entrada), pero sin ir tan lejos, podemos imaginarnos una botella.
El tapón, al ser plano, posee una curvatura plana. Asimismo, los tramos quasi rectos de la misma (que se aproximan a un cilindro) son casi de curvatura parabólica, en el sentido de que:
- |ς| ≈ 0.
Los picos del fondo de la botella son elípticos, pues los planos tangentes a ellos dejan toda la botella a un lado, y por último, los “hundimientos” que hace el diseño de la botella son hiperbólicos.