
Un agujero negro emite radiación como un cuerpo caliente a la temperatura de Hawking. Si su valor es muy alto, la radiación de Hawking consiste en partículas de todo tipo (fotones, gravitones, bosones vectoriales, bosones de Higgs, leptones y hadrones), pero si su valor es “bajo” solo emite fotones y gravitones. El vacío cerca del horizonte de sucesos produce pares de partícula-antipartícula virtuales en los que una de las partículas penetra en el agujero negro y la otra escapa, produciendo la radiación.
Esta imagen es falsa. Hay varias razones pero la más importante es que la longitud de onda de las partículas absorbidas y emitidas es comparable al tamaño del agujero negro (λ ≈ 2 G M/c²); por tanto, imaginar que estas partículas están localizadas en el entorno del horizonte de sucesos no tiene ningún sentido físico. Estas partículas son tan grandes como el propio agujero negro y no tiene ningún sentido preguntarse dónde están, igual que un electrón en un átomo tiene una longitud de onda comparable al propio átomo y no podemos saber dónde está el electrón dentro del átomo.

La imagen de un par partícula-antipartícula en el entorno del agujero negro fue introducida por Hawking, pero no se puede olvidar que la longitud de onda más probable de estas partículas es comparable al radio de Schwarschild.
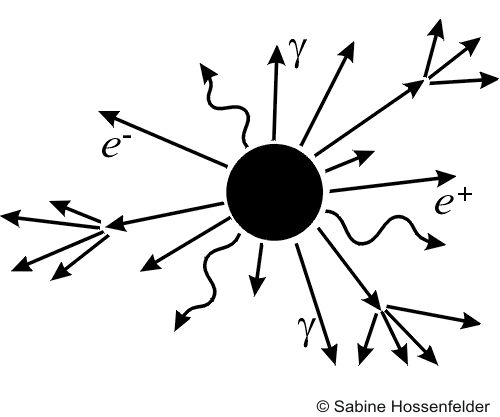
Por tanto, no tiene sentido imaginar las partículas como “pequeñas bolitas” cerca den un horizonte de sucesos enorme (como se muestra en esta figura).
Las partículas tienen una longitud de onda λ tan grande como el agujero negro y se separan una distancia similar a λ, evitando aniquilarse entre sí gracias a las fuerzas de marea gravitatorias. De hecho, Birrell y Davies destacan que el concepto de partícula utilizado en física de partículas, una excitación localizada de un campo cuántico en un espaciotiempo plano, no está bien definido para las partículas de la radiación de Hawking que están “localizadas” en todo el área del agujero negro y, por tanto, están sometidas a un espaciotiempo muy curvado. Las partículas de la radiación de Hawking se comportan como partículas (en el sentido usual de la física de partículas) muy lejos del horizonte de sucesos (a una distancia de muchas longitudes de onda, es decir, muchas veces el radio de Schwarschild).
Por supuesto, en el entorno del horizonte de sucesos de un agujero negro suficientemente grande el espaciotiempo es muy plano (más plano cuanto más masivo es) con lo que el concepto de partícula es aplicable para partículas y/o objetos con un tamaño mucho más pequeño que el radio de Schwarschild.
Una persona que entrase en un agujero negro supermasivo no notaría nada al cruzar el horizonte de sucesos (pues las fuerzas de marea gravitatorias son muy pequeñas). Pero esta persona tampoco notaría la existencia de la radiación de Hawking, ya que su tamaño (el de la persona) es infinitesimal comparado con la longitud de onda de las partículas de la radiación de Hawking (cuya longitud de onda puede ser similar al radio de la órbita de Mercurio alrededor del Sol).
Para detectar la radiación de Hawking se requiere un detector con un tamaño similar a la longitud de onda (que actuaría como antena). Esta es la razón del porqué un observador que caiga en un agujero negro de gran masa no puede observar la radiación de Hawking.
Las partículas emitidas por un agujero negro tienen un espectro térmico (de cuerpo negro) a la temperatura de Hawking T= ℏ c³/(8π G M k); esta temperatura es muy pequeña para un agujero negro macroscópico (millones de veces inferior a la del fondo cósmico de microondas para agujeros negros astrofísicos). Sin embargo, esta temperatura es enorme para agujeros negros microscópicos. ¿Qué tipo de partículas puede emitir un agujero negro?
Un agujero negro puede emitir partículas tanto sin masa como con masa, en función de su temperatura, pero la emisión de partículas con masa m menor que la temperatura del agujero negro está exponencialmente suprimida, en la práctica no se emiten partículas con masa m ≪ ℏ c/(8π GM), es decir, c²/k≪ ℏ c³/(8π GM k).
En los experimentos ATLAS y CMS del LHC en el CERN se está buscando la señal de la desintegración de microagujeros negros con una masa en la escala de los TeV (teraelectrónvoltio).
Estos agujeros solo pueden existir si existen dimensiones extra en el espaciotiempo y no encontrarlos nos ayuda a descartar estas dimensiones extra en la escala de los TeV.
Para un microagujero negro tipo Schwarschild con una masa de unos pocos TeV, la radiación de Hawking está formada por un 72% de quarks y gluones, un 11% de leptones, un 8% de bosones vectoriales W y Z, un 6% de neutrinos y gravitones, un 2% de bosones de Higgs y un 1% de fotones (suponiendo que no existen más partículas que las conocidas a día de hoy). Los interesados en el cálculo pueden consultar, por ejemplo, Steven B. Giddings, Scott Thomas, “High Energy Colliders as Black Hole Factories: The End of Short Distance Physics,” Phys. Rev. D 65: 056010, 2002 [arXiv:hep-ph/0106219]).
Por tanto, un microagujero negro emite todo tipo de partículas, es decir, cualquier cosa que gravite.
Sin embargo, un agujero negro astrofísico (con una masa estelar) solo emite fotones y gravitones; para una masa similar a la del Sol emite un 90% de fotones y un 10% de gravitones.
En el libro de Birrell y Davies se cita un cálculo de Page (1976), según el cual la producción de electrones y positrones se inicia cuando el agujero negro tiene una masa M < 50×10¹³ kg, o una temperatura mayor de mil millones de Kelvin (partículas con mayor masa requieren masas más pequeñas, temperaturas más altas).
Para agujeros negros con una masa M ≫ 50×10¹³ kg solo se emiten partículas con menor masa que el electrón o partículas sin masa.
En el cálculo original de Page (1976), cuando se pensaba que los neutrinos no tenían masa y que sólo había dos sabores de neutrinos, se estimó que se emitirían un 81% de neutrinos (repito, dos especies sin masa), un 17% de fotones y un 2% de gravitones; en el caso de que hubiera tres especies de neutrinos sin masa totalizarían un 87% de las partículas emitidas.
Sin embargo, como los neutrinos tienen masa, hay que rehacer el cálculo de Page y solo se emitirían en dicho caso fotones y gravitones.
Como aún no conocemos la masa de los neutrinos el cálculo detallado es difícil, pero los interesados en una estimación “razonable” pueden consultar Daniel Bambeck, William A. Hiscock, “Effects of nonzero neutrino masses on black hole evaporation,” Class. Quant. Grav. 22: 4247-4252, 2005 [arXiv:gr-qc/0506050].

Sólo en circunstancias excepcionales el concepto de partícula en un espaciotiempo curvo corresponde a la imagen física intuitiva de una partícula subatómica. Por tanto, en general, no hay ninguna definición natural del concepto de partícula y Birrell y Davies, en su capítulo 6 de su libro de 1982, se concentran en el cálculo cuántico del valor del tensor de energía-momento del campo.
De hecho, la mejor manera de explicar la radiación de Hawking es utilizando el valor del tensor energía-momento, que está bien definido en el entorno del horizonte de sucesos y cuyo valor cuántico finito se puede calcular mediante renormalización (o regularización) dimensional de la constante de acoplo gravitatoria.
Por supuesto, La gravedad cuántica no es renormalizable y un cálculo naïve da un resultado infinito, pero se puede desarrollar una técnica de renormalización (regularización) dimensional de la constante de acoplo de la gravedad que permite obtener un valor finito. La técnica se basa en considerar la aproximación cuasiclásica hasta un bucle (loop), en la que la gravedad se considera clásica, pero los campos de materia y los gravitones se consideran cuánticos. Birrell y Davies hablan de una definición adiabática del concepto de partícula.
¿Por qué el concepto de partícula no es bueno para describir la física cuántica de los agujeros negros?
Birrell y Davies nos lo cuentan en la sección 3.5 de su libro. Para poder definir el concepto de partícula como excitación cuántica de un campo, tenemos que definir primero el concepto de vacío del campo. En un espaciotiempo de Minkowski el concepto de vacío (y de partícula) se pueden definir de forma global. Sin embargo, en una espaciotiempo curvo el vacío solo se puede definir de forma local y cada observador acelerado tiene su propia descripción de lo que es el vacío. Una región del espaciotiempo “vacía” para un obsevador acelerado puede contener partículas para otro observador. Por ello, en un espaciotiempo curvo general no hay una definición natural de partícula, aunque existe en casos particulares; por ejemplo, en un espaciotiempo de Robertson-Walker se puede definir un vacío común a todos los observadores comóviles (que observan la expansión del universo como isótropa).
En este sentido, el vacío y las partículas son conceptos adiabáticos.
Por supuesto, que nadie se lleve las manos a la cabeza. Cuando se dice que el concepto de partícula no está bien definido en un espaciotiempo curvo se está hablando de partículas cuya longitud de onda es lo suficientemente grande como para notar la curvatura del espaciotiempo.
Para partículas de longitud de onda pequeña, el espaciotiempo es localmente plano y el concepto de partícula es perfectamente aplicable, pero para dichas partículas la gravedad es una interacción tan extremadamente débil que sus efectos son despreciables.
Utilizando el tensor de energía-momento, Birrell y Davies nos dice que la radiación de Hawking y la pérdida de masa (y área) de los agujeros negros se puede explicar por la absorción de energía negativa; hay un flujo de energía negativa hacia el interior del agujero negro compensado por un flujo de energía positiva hacia el exterior en forma de partículas (la radiación de Hawking).
Esta descripción de la termodinámica de los agujeros negros entre lo clásico y lo cuántico ha sido revisada durante la década de los 1990 gracias a las ideas de la teoría de cuerdas y/o la gravedad cuántica de bucles.
Lo bonito de la idea es que un espaciotiempo curvado en expansión emite radiación y si está muy caliente emite todos los tipos de partículas conocidas.
La gravedad cuántica (en la aproximación semiclásica presentada por Birrell y Davies) explica de manera natural la producción de partículas en los primeros instantes de la gran explosión (big bang).
Un espacio tiempo acelerado durante la inflación cósmica y muy caliente “emite” todo tipo de partículas.
Todas las partículas que conocemos.
http://francis.naukas.com
http://francis.naukas.com