Contar todas las partículas (fundamentales) conocidas es un ejercicio fácil.
Las partículas son excitaciones localizadas de campos cuánticos, por lo que parece mejor contar las componentes de dichos campos.
También es fácil, aunque hay algunas sutilezas que hay que tener en cuenta.
Las partículas conocidas son de dos tipos, fermiones (espín 1/2) y bosones (espín 0, 1 y 2); incluyo el gravitón (espín 2), pero no el gravitino (espín 3/2), siendo ambas partículas hipotéticas aún no descubiertas, porque hay evidencia indirecta de la existencia de las ondas gravitatorias, pero no la hay de la supersimetría.
Empezaremos contando los fermiones.
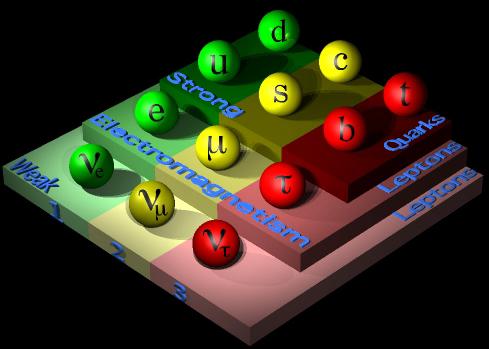
Como muestra la figura de arriba, los fermiones se dividen en tres generaciones de leptones y quarks; en cada generación hay dos leptones, uno cargado (tipo electrón) y otro neutro (tipo neutrino), y hay dos quarks, uno tipo arriba y el otro tipo abajo. Los tres leptones cargados (electrón, muón y tauón) tienen asociado cada uno un neutrino; los seis quarks son llamados arriba, u (up), abajo, d (down), extraño, s (strange), encanto, c (charm), fondo, b (bottom), y cima, t (top).
La figura de arriba muestra 12 bolitas que corresponden a 12 partículas (aunque faltan sus correspondientes 12 antipartículas).
Sin embargo, hay que recordar que los quarks tienen carga de color (con tres valores posibles), luego en lugar de 6 quarks tenemos 18 (y sus correspondientes 18 antiquarks). Por tanto, un cálculo naïve (ingenuo) nos dice que hay 24 fermiones y 24 antifermiones, un total de 48 partículas.
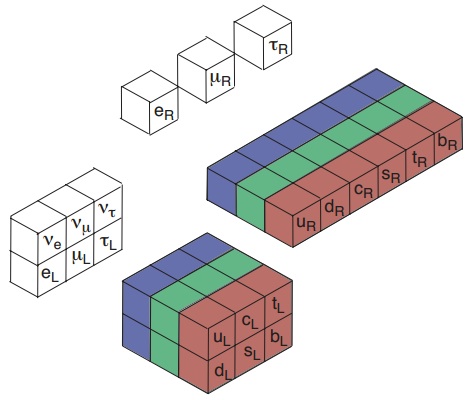
El cálculo anterior del número de fermiones no tiene en cuenta la quiralidad del modelo estándar. Sabemos que hay electrones levógiros (izquierdos, L) y dextrógiros (derechos, R), pero sólo hemos observado neutrinos levógiros.
De hecho, las componentes levógiras se agrupan en parejas (dobletes), pero las dextrógiras no se emparejan (singletes). Por todo ello es mucho mejor contar el número de componentes de los campos que el número de partículas.
Un fermión de Dirac tiene cuatro componentes agrupadas en dos parejas, una pareja representa la partícula y la otra su antipartícula; en cada pareja hay una componente levógira y otra dextrógira.
Los tres leptones cargados y los 18 quarks son campos fermiónicos de Dirac y cada uno tiene cuatro componentes. Sin embargo, no sabemos si los leptones neutros (neutrinos) son fermiones de Dirac (los neutrinos dextrógiros no han sido observados en los experimentos) o de Majorana (un fermión de Majorana tiene sólo dos componentes y es idéntico a su antipartícula); si todo va bien con los nuevos experimentos en curso, en un par de años deberíamos saberlo.
Por tanto, si los neutrinos son fermiones de Dirac tenemos 4 × 18 + 4 × 3 + 4 × 3 = 96 componentes de campos fermiónicos (de las que 6 aún no han sido observadas en los experimentos), y si son fermiones de Majorana tenemos 4 × 18 + 4 × 3 + 2 × 3 = 90 componentes (siendo los neutrinos y los antineutrinos la misma partícula).
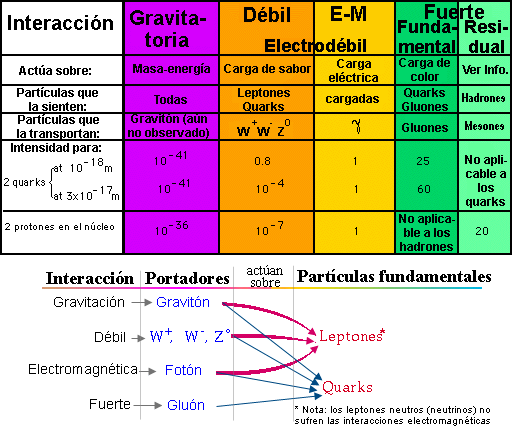
Ahora le toca el turno a los bosones.
A baja energía, tras la rotura espontánea de la simetría electrodébil, tenemos un bosón escalar (espín cero), el bosón de Higgs, doce bosones vectoriales (espín uno), el fotón, los bosones Z, W− y W+, y 8 gluones, y creemos que existe un bosón tensorial (espín dos), el gravitón, aún no observado de forma directa.
En total tenemos 13 bosones; no hay que contar las antipartículas porque todos los bosones que son neutros son idénticos a su antipartícula, y la antipartícula del W− es el W+, y viceversa.
Contemos ahora el número de componentes de los bosones.
El campo de un bosón escalar neutro (como el Higgs) tiene una sola componente (y por ello es idéntico a su antipartícula); los bosones escalares cargados (como los Higgs predichos por la supersimetría) tienen dos componentes (el de carga positiva es la antipartícula del de carga negativa y viceversa).
Por tanto, el Higgs del modelo estándar cuenta como una sola componente.
El campo de un bosón vectorial sin masa (como el fotón y el gluón) tiene dos componentes (transversales al momento) y el de un bosón vectorial con masa (como los bosones W y Z) tiene tres componentes (dos transversales y una longitudinal). Por tanto, en el modelo estándar tenemos 2 + 8 × 2 + 3 × 3 = 27 componentes de campos vectoriales.
El gravitón es un bosón de espín dos sin masa y por tanto tiene dos componentes (que son transversales al momento).
Un gravitón con masa tiene cinco componentes (llamadas polarizaciones) ya que es un bosón de espín dos.
Esto último puede resultar sorprendente a algunos lectores, pero se sabe desde el artículo de Fierz y Pauli (1939); el tensor métrico en cuatro dimensiones es simétrico, luego tiene 10 componentes, pero no son linealmente independientes entre sí, ya que se cumplen las identidades de Bianchi, que eliminan cuatro componentes, y la física cuántica requiere que su traza sea nula, lo que elimina una componente más.
Por cierto, Boulware y Deser (1972) afirmaron que las ecuaciones de un gravitón masivo deben incluir un término no lineal que invalida la condición de traza nula, con lo que el gravitón masivo debería tener seis componentes (o polarizaciones); pero según el único candidato firme a teoría cuántica de la gravedad, la teoría de cuerdas, el gravitón tiene cinco componentes.
Finalmente, como nos recordó Amarashiki en Twitter, en D dimensiones el tensor métrico (una matriz real simétrica) tiene D(D+1)/2 componentes independientes, el campo de un gravitón sin masa tiene D(D−3)/2 componentes y el de un gravitón masivo D(D−1)/2 − 1; por ejemplo, en D=11 dimensiones el campo de un gravitón sin masa tiene 44 componentes.
Resumiendo el número de componentes de los campos bosónicos conocidos es de 1+27+2 = 30. Siendo el número total de componentes (fermiónicas y bosónicas) es de 126.
Este número puede ocultar alguna simetría (como proponen Alejandro Rivero y muchos otros físicos), o bien puede ser una simple casualidad. Me permito argumentar a favor de esta última idea.

En cuanto al número de fermiones, no tenemos ningún argumento físico razonable que explique por qué hay sólo tres generaciones de partículas.
Por ello, en los experimentos del LHC se siguen buscando partículas de una posible cuarta generación (como también se buscaron en Tevatrón y en LEP).
Sin embargo, hay poca esperanza de encontrarlas. Sabemos que el neutrino de la cuarta generación debe tener una masa mayor de 45 GeV, luego será un neutrino muy diferente a los otros tres.
Los tests de precisión electrodébil apuntan a la diferencia de masa entre la pareja de quarks de cuarta generación sea pequeña, menor que la masa del bosón W, m(t’) − m(b’) < m(W), con lo que sus desintegraciones más probables son t’→Wb y b’→tW, en las que han sido buscados sin éxito reultando m(t’)>650 GeV y m(b’)>660 GeV ambos al 95% CL (Andrew Ivanov (ATLAS, CMS), “Limits on Fourth Generation Fermions,” arXiv:1308.3084, Subm. 14 Agu 2013).
Finalmente, el estudio de los canales de desintegración del Higgs también descarta una cuarta generación de quarks con masas menores de de unos 650 GeV.
Tampoco sabemos si existen o no nuevos bosones vectoriales neutros, Z’ (Z-prima), o cargados, W’ (W-prima), que corresponderían a nuevas simetrías U(1) y SU(2), respectivamente, a incorporar al modelo estándar.
Las búsquedas de estos bosones en el LHC los descartan con masas inferiores a 1 TeV (en algunos canales de búsqueda de hasta 2 TeV).
Tampoco sabemos si existen nuevos bosones escalares (nuevos bosones de Higgs). Y no he mencionado la posibilidad de partículas más exóticas.
Sólo hemos explorado el modelo estándar por debajo de un 1 TeV (y todavía no de forma completa). En mi opinión, como la de muchos físicos, pensar que lo que hemos descubierto hasta ahora es lo único que existe es muy discutible.
Otra cosa muy diferente es que dichos descubrimientos estén a la vuelta de la esquina.
Acabamos de iniciar el siglo XXI y todavía no hemos completado el modelo estándar (aún no conocemos muchas de las propiedades de los neutrinos y hay muchas predicciones del modelo estándar que aún no han sido verificadas).
Hay que darle tiempo al tiempo.
http://francis.naukas.com
http://francis.naukas.com