
El teorema de Pitágoras es sin duda la más conocida de todas las matemáticas.
Pero, ¿quién sabe realmente el show de la nada?
Sin embargo, debe haber varios cientos de maneras de hacerlo!
Por mi parte, nunca me las arreglé para aceptar una sola manifestación ... hasta que vì a uno de los más hermosos de todos para mi gusto particularmente bueno: una demostración del curso de física ya que utiliza
el análisis dimensional !
Considere la posibilidad de un triángulo rectángulo.
Está perfectamente caracterizada por los datos de la hipotenusa (llamada entonces C) y uno de sus ángulos agudos (llamar  ).
).
Si te doy C  , puede reconstruir el triángulo inequívoca.
, puede reconstruir el triángulo inequívoca.

Consideremos ahora el área de un triángulo rectángulo.
Desde un triángulo de este tipo se caracteriza por completo y C  ,
,
hay una función
que da el valor de esta zona. Si quería, podía encontrar la fórmula exacta para esta función, pero no lo necesitaré.
Hagamos un poco de análisis dimensional :
el área  es el cuadrado de una longitud, C es la longitud hipotenusa,
es el cuadrado de una longitud, C es la longitud hipotenusa,
y  es un número sin dimensiones.
es un número sin dimensiones.
La única manera de que la unidad de pegamento es que la fórmula para el área de un triángulo rectángulo tiene la siguiente forma
donde  es una función que no necesitaba mirar para saber.
es una función que no necesitaba mirar para saber.
Ahora considere el siguiente diagrama, donde voy una hipotenusa C triángulo y sin ángulo  .
.
En el dibujo, también me tracé su altura.
Ya que el triángulo de altura compartir nuestros dos pequeños triángulos rectángulos hipotenusa respectivos A y B, cada uno con un ángulo  .
.
Puesto que el área del triángulo grande es igual a la suma de ese pequeño, podemos escribir:
Me simplifica  y voila:
y voila:
No está mal, ¿verdad?
Por supuesto, los matemáticos se esfuerzan en gritar,
pero no me importa!
Para aquellos que quieran profundizar, podemos ver que lo que la validez física del razonamiento es que no hay ningún problema en la otra cantidad de dimensión longitud.
Tenga en cuenta que ya no funcionaría en el espacio curvo, por ejemplo, para una pista en una esfera, que tiene un triángulo longitud natural:
el radio de curvatura.
Por otra parte, la fórmula para el área de un triángulo esférico es de gran belleza.
Recuerdo haber intentado encontrarla (sin saberlo) y cuando el resultado apareció ante mis ojos me fascinó: una esfera de radio 1, el área de un triángulo esférico es igual a la suma de su ángulos (menos 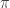 ) !
) !

