
I just uploaded to the arXiv a preprint of my paper on extended eigenvalues for Cesàro operators. This is joint work with Fernando León-Saavedra (Cádiz), John Petrovic (Michigan) and Omid Zabeti (Iran).
A complex scalar  is said to be an extended eigenvalue of a bounded linear operator
is said to be an extended eigenvalue of a bounded linear operator 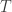 on a complex Banach space if there is a nonzero operator
on a complex Banach space if there is a nonzero operator 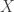 such that
such that  Such an operator
Such an operator 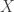 is called an extended eigenoperator of
is called an extended eigenoperator of 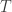 corresponding to the extended eigenvalue
corresponding to the extended eigenvalue 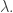
The purpose of this paper is to give a description of the extended eigenvalues for the discrete Cesàro operator 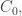 the finite continuous Cesàro operator
the finite continuous Cesàro operator  and the infinite continuous Cesàro operator
and the infinite continuous Cesàro operator 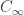 defined on the complex Banach spaces
defined on the complex Banach spaces 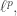
![L^p[0,1] L^p[0,1]](http://s0.wp.com/latex.php?latex=L%5Ep%5B0%2C1%5D&bg=ffffff&fg=333333&s=0) and
and  for
for  by the expressions
by the expressions
It is shown that the set of extended eigenvalues for  is the interval
is the interval  for
for  it is the interval
it is the interval ![(0,1], (0,1],](http://s0.wp.com/latex.php?latex=%280%2C1%5D%2C&bg=ffffff&fg=333333&s=0) and for
and for 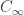 it reduces to the singleton
it reduces to the singleton 