martes, 29 de julio de 2014

Café matemático: Una función patológica (34070)


El objeto de este post es una función 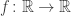f \colon \mathbb R \to \mathbb R que admite derivadas de todos los órdenes y tal que f^{(n)}(0)=0 para todo n \in \mathbb N, aunque f(x)>0 para todo x \neq 0. 
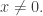
Así, resulta imposible aproximar la función f mediante sus polinomios de Taylor en el origen, pues todos los polinomios de Taylor de f en el origen son nulos, aunque f no se anula idénticamente.
Sea 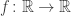f \colon \mathbb R \to \mathbb R la función definida mediante la expresión
\displaystyle{f(x)= \left \{ \begin{array}{rl} e^{-1/x^2}, & \text{ si } x \neq 0\\ 0, & \text{ si } x=0\end{array} \right.}
Está claro que f es continua en el origen. A continuación probamos que f es derivable en el origen. El siguiente resultado se obtiene al aplicar sucesivas veces la regla de L’Hôpital
Lema. \displaystyle{\quad \lim_{t \to \infty} \frac{t^\alpha}{e^t}=0} para todo \alpha \in \mathbb R.
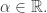
Aplicando el lema tenemos
\displaystyle{f^\prime(0)= \lim_{h \to 0} \frac{f(h)-f(0)}{h}= \lim_{h \to 0} \frac{e^{-1/h^2}}{h} = \lim_{h \to 0} \frac{1/h}{e^{1/h^2}} = \lim_{t \to \infty} \frac{t^{1/2}}{e^t}=0.}
Además, si x \neq 0 entonces se sigue de la regla de la cadena que
\displaystyle{f^\prime(x)=\frac{2}{x^3} e^{-1/x^2},}
y por lo tanto
\displaystyle{f^{\prime \prime}(0)= \lim_{h \to 0} \frac{f^\prime (h)-f^\prime (0)}{h}= \lim_{h \to 0} \frac{e^{-1/h^2}}{h} = \lim_{h \to 0} \frac{2/h^4}{e^{1/h^2}} = \lim_{t \to \infty} \frac{2t^2}{e^t}=0.}
Además, si x \neq 0 entonces
\displaystyle{f^{\prime \prime}(x)=-\frac{6}{x^4} e^{-1/x^2} + \frac{2}{x^6}e^{-1/x^2},}
y por lo tanto
\displaystyle{f^{\prime \prime \prime}(0)= \lim_{h \to 0} \frac{f^{\prime \prime} (h)-f^{\prime \prime} (0)}{h}= \lim_{h \to 0} \frac{1}{h} \left ( -\frac{6}{h^4} e^{-1/h^2} + \frac{2}{h^6}e^{-1/h^2} \right )=}
\displaystyle{ = \lim_{h \to 0} \frac{-6/h^5}{e^{1/h^2}} + \frac{2/h^7}{e^{1/h^2}}=- 6 \lim_{t \to \infty}\frac{t^{5/2}}{e^t} + 2 \lim_{t \to \infty} \frac{t^{7/2}}{e^t}=0.}
Se puede probar por inducción que f^{(n)}(0)=0 para todo n \in \mathbb N.
Publicado por en