miércoles, 29 de octubre de 2014

Mecánica de Fluidos — Definiciones y aparato matemático

A lo largo de una serie de entradas presentaremos los fundamentos más básicos de la mecánica de fluidos en su formulación clásica o macroscópica, esto es, basada en la hipótesis del medio continuo. 
Dicha hipótesis asume que las longitudes características del movimiento estudiado son mucho mayores que las distancias intermoleculares del medio que estamos analizando; dicho de otro modo: por muy cerca que miremos nunca veremos el fluido como si estuviera compuesto por moléculas individuales.
El estudio de la mecánica de fluidos es fundamental en muchos aspectos de la física aplicada y de la ingeniería ya que, a poco que nos paremos a pensar, nos damos cuenta de que:
  • El 70% (aproximadamente) de la superficie de la Tierra está cubierta por agua.
  • El 100% de la superficie de la Tierra está cubierto por aire.
Los dos puntos anteriores muestran que todo aquello que desarrolla su movimiento en este planeta lo hace sumergido en, o rodeado por, un fluido.
Más allá del ejemplo anterior, que es un poco de perogrullo, el interés teórico del estudio de la mecánica de fluidos es enorme. Próximamente veremos que uno de los campos de investigación más activos hoy en día dentro del ámbito de la física clásica es el estudio de la turbulencia en el flujo de fluidos, ya que se trata de un problema que a día de hoy no está totalmente cerrado. Más allá de la turbulencia, existen múltiples líneas de investigación en el tema de la micro y la nano-fluídica, así como en el campo de la física de flujos eléctricamente cargados. Por último, si nos vamos a las escalas más grandes, con la mecánica de fluidos podemos estudiar tanto la dinámica de la atmósfera como de las grandes corrientes oceánicas. A escalas aun mayores, la mecánica de fluidos nos sirve para comprender el movimiento a gran escala de los plasmas en interior de las estrellas.
¿Qué es un fluido? Fluidos newtonianos y no-newtonianos
Pero antes de todo lo anterior debemos pararnos un momento. Para empezar, lo más conveniente es que definamos qué es un fluido. Bien, aquí va:

Un fluido es un medio continuo que que es incapaz de resistir esfuerzos cortantes.
Bueno, ahora vayamos por partes. Lo del medio continuo ya lo hemos comentado antes. Fijémonos entonces en la segunda parte de la definición, y más concretamente en lo de esfuerzos cortantes. Para ello, imaginemos que tenemos una superficie; en principio esta superficie puede tener cualquier forma, sin embargo, para fijar ideas, centrémonos en un plano. En cualquier punto de ese plano podemos definir un sistema de ejes en el que hay un vector normal (perpendicular) a la superficie y dos vectores tangentes a la superficie. Algo como esto:
Figura1
Ahora imaginemos que sobre la superficie aplicamos una fuerza. En cada punto de la superficie podremos entonces descomponer la fuerza aplicada en las componentes que vienen dadas por el sistema de ejes que hemos definido antes. Si lo hacemos veremos algo como esto (las componentes de la fuerza aplicada se representan como segmentos sobre los ejes en vez de como flechas para no embarrullar demasiado la figura):
Figura2
Por último podemos sumar las dos componentes tangentes al plano para calcular su resultante:

Figura3
Como vemos, hemos descompuesto la fuerza aplicada, que a partir de ahora llamaremos esfuerzo (ya que en realidad una fuerza nunca se aplica sobre un punto, sino que se distribuye sobre una superficie, por muy pequeña que sea), en dos componentes (notemos que representamos los vectores por caracteres en negrita):

  • El esfuerzo normal, que es perpendicular a la superficie, y que en la figura se denota por \boldsymbol{f_n}
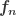
  • El esfuerzo cortante, que es tangente a la superficie, denotado por \boldsymbol{f_\tau}.
Ahora que tenemos claro lo que es el esfuerzo cortante podemos volver a la definicíón de fluido. Para ello, imaginemos que tenemos un cubito de hielo, sólido, apoyado sobre una mesa. El cubito, normalmente, estará sometido a su peso, que se distribuye de manera uniforme en su volumen:
Figura4
Si hacemos un pequeño esfuerzo, podemos ver cómo el cubito de hielo está lleno de vectores apuntando hacia el suelo. Si lo partimos por la mitad, podemos ver claramente como en cada una de las paredes verticales que han aparecido en nuestro corte hay una componente cortante (en este caso no hay componentes normales aplicadas sobre las superficies verticales). Por tanto, el cubito de hielo está soportando esfuerzos cortantes en todo su dominio. Como respuesta a esos esfuerzos, el cubito se comba imperceptiblemente, deformándose. Esto es lo característico de los sólidos: Ante una solicitación, tienen la capacidad de deformarse para responder a ella (la famosa ley de Hooke).

Ahora imaginemos que tenemos un cubito de agua líquida sobre la mesa. Efectivamente, hagamos el esfuerzo de imaginarlo, ya que el agua líquida se desparrama en cuanto tiene oportunidad. El imaginario cubito de agua no puede soportar los esfuerzos cortantes que tiene dentro, por lo que se nos derrama por toda la mesa, poniéndolo todo perdido. Esto es lo que define un fluido, o mejor, es lo que distingue a los sólidos de los fluidos.
Otra forma de decir esto es que, al contrario que los sólidos, los fluidos no presentan resistencia a la deformación.
Además de lo anterior, experimentalmente se observa que los fluidos, pese a no oponerse a la deformación, sí que se oponen a la velocidad con la que se deforman (después de todo el agua no se desparrama a una velocidad infinita). Para ver esto, pensemos que tenemos una lámina de fluido encerrada entre dos paredes, estando la inferior quieta y moviéndose la superior con una velocidad \boldsymbol{v}. En estas condiciones, la parte del fluido que está en contacto con la pared inferior posee una velocidad nula, mientras que la que está en contacto con la pared superior se mueve también a velocidad \boldsymbol{v}.
 En el interior del dominio, aparecerá un perfil de velocidades que irá desde la velocidad nula en la pared inferior hasta la velocidad \boldsymbol{v} en la superior.
Figura5
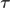Como vemos, el perfil de velocidades cambia con la altura, por lo que podemos calcularle la derivada. Al mismo tiempo, podemos calcular el esfuerzo cortante sobre la pared inferior (que es la que “retiene” al fluido. Si medimos esto experimentalmente y comparamos los valores obtenidos, veremos que se cumple una relación del tipo (\boldsymbol{\tau} denota el esfuerzo cortante, e 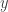y denota la coordenada vertical, respecto a la que derivamos):

\boldsymbol{\tau}\propto \left(\frac{d\boldsymbol{v}}{dy}\right)_{ y=0}
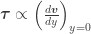Esta es la expresión matemática, denominada de forma más exacta Ley de Comportamiento que muestra lo que hemos afirmado antes: La resistencia del fluido a la velocidad de deformación se manifiesta a través de la relación proporcional entre la variación del perfil de velocidades y el esfuerzo cortante.
La ley de comportamiento anterior puede manifestarse de varias formas, según sea el fluido analizado. Toda la casuística posible se divide en dos grandes grupos:
  • Aquellos en las que la proporcionalidad se manifiesta mediante una ley lineal.
  • Aquellos en los que dicha ley es no lineal.
En el caso de la ley lineal de comportamiento, la relación es de la forma:
\boldsymbol{\tau} = \mu \left(\frac{d\boldsymbol{v}}{dy}\right)_{y=0}
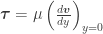Donde la constante de proporcionalidad \mu se llama viscosidad dinámica del fluido. Sustancias como el agua líquida o el aire tienen una ley de comportamiento de ese tipo. A todos los fluidos que siguen una ley lineal se les llama Fluidos Newtonianos.
Si la ley de comportamiento no es lineal, entramos en el mundo de los Fluidos No Newtonianos. Un fluido no newtoniano muy común es la pasta de dientes (todos hemos comprobado como no empieza a fluir hasta que la fuerza con la que apretamos el tubo no supera un cierto valor). La casuística (a menudo mucho más contraintuitiva que la de los fluidos newtonianos) de los fluidos no newtonianos responde a una descripción matemática mucho más compleja que la de los newtonianos, y tradicionalmente su estudio es objeto de una disciplina aparte denominada Reología.
A lo largo de esta serie de entradas nos ceñiremos a la descripción del movimiento de los fluidos newtonianos.

Descripción lagrangiana y euleriana. Derivada sustancial, material o convectiva

A la hora de estudiar el movimiento de los fluidos pueden adoptarse dos grandes marcos de descripción:
Por una parte podríamos usar una descripción en la que la única variable independiente a la hora de analizar la evolución de una magnitud característica cualquiera del campo fluido, \phi, sea el tiempo:
\phi=\phi(t)
En este tipo de descripción, tradicionalmente denominada lagrangiana, podemos asimilar el estudio del movimiento del fluido al análisis de la evolución temporal de las trayectorias de todos los “puntos materiales” que forman parte del medio continuo. Por sus características, la variable fundamental a calcular en este tipo de descripción es la posición de las partículas fluidas.
Sin embargo, salvo en situaciones muy particulares (análisis de sedimentación, transporte de partículas, dispersión de aerosoles, etc.), esta descripción no es la habitualmente utilizada. No es difícil imaginar el por qué: La descripción del movimiento de cada partícula provoca que la complejidad matemática del problema crezca tanto que su uso para fines prácticos está totalmente desaconsejado. En su lugar, podemos usar una descripción en la que tanto el tiempo, como la posición, sean variables independientes. De este modo, una variable cualquiera se definiría mediante una función del tipo:
\phi=\phi(\boldsymbol{r},t)
Esta es la conocida como descripción euleriana, que es la que habitualmente se utiliza para plantear las ecuaciones de la mecánica de fluidos. En esta descripción, resolver el problema equivale a encontrar el campo de velocidades.
Una vez expuestas las descripciones posibles, es lícito preguntarse cómo se define el cambio de una magnitud en cada una de ellas, o lo que es lo mismo, cómo se calculan las derivadas. En el caso de la descripción lagrangiana la derivada simplemente es la derivada temporal:
\dfrac{d\phi}{dt}
En el caso de la descripción euleriana, el cálculo de las derivadas no es tan inmediato. Efectivamente, a la hora de describir cómo cambia una magnitud del campo fluido, debemos tener en cuenta que posición y tiempo son variables independientes. Si tenemos esto en cuenta, y calculamos la variación temporal de una magnitud asociada a un punto material a medida que dicho punto material se mueve, debemos operar como sigue:
d\phi = \phi(\boldsymbol{x}+d\boldsymbol{x},t+dt)-\phi(\boldsymbol{x},t)
d\phi = d\boldsymbol{x} \cdot \nabla\phi + \frac{\partial\phi}{\partial t} dt
\frac{d\phi}{dt} = \frac{\partial\phi}{\partial t} + \boldsymbol{v} \cdot \nabla\phi
En la expresión anterior se ha tenido en cuenta que \frac{d\boldsymbol{x}}{dt} es precisamente la velocidad a la que se mueve la partícula que estamos siguiendo, que no es otra que la velocidad a la que se mueve el fluido.
Finalmente, para distinguirla de las derivadas convencionales (no parciales) respecto al tiempo, hacemos el siguiente cambio de notación: \frac{d\phi}{dt} \equiv \frac{D\phi}{Dt}, para representar nuestra derivada, que a partir de ahora llamaremos derivada siguiendo al punto material o, mejor aún, derivada sustancial. También conocida como derivada material o derivada convectiva.
El operador de la derivada sustancial es, ateniéndonos al desarrollo anterior, el siguiente:
\frac{D}{Dt} = \frac{\partial}{\partial t} + \boldsymbol{v} \cdot \nabla
La interpretación de la derivada sustancial puede resultar un tanto extraña, pero rápidamente se aclara si tenemos en cuenta que, para calcularla, y teniendo siempre presente que posición y tiempo son variables independientes, en todo momento hemos seguido a un punto material que se mueve con el fluido; por tanto, las componentes del campo fluido cambiarán no sólo por que el tiempo avance, sino también porque la posición de la partícula que hemos ido siguiendo ha ido cambiando.
Una última puntualización sobre la notación y la interpretación del operador que hemos definido. Como hemos visto, la derivada sustancial tiene dos sumandos. El primero de ellos:
\frac{\partial}{\partial t} — Se denomina aceleración local, y, como es natural, recoge las variaciones en las magnitudes al avanzar el tiempo.
\boldsymbol{v} \cdot \nabla — Este término tiene la información de las derivadas espaciales y recoge las variaciones en las magnitudes cuando pasamos de un punto a otro del dominio fluido.
Conviene observar que el término de la derivada convectiva introduce una no linealidad en las ecuaciones que estamos tratando de plantear. A ese término se debe, fundamentalmente, la tremenda variedad y complejidad de los movimientos de los fluidos, así como las soluciones, a menudo caóticas, de los problemas que se plantean en esta disciplina.

El teorema del transporte de Reynolds

Acabamos de presentar una de las herramientas matemáticas fundamentales en las que se basa el desarrollo de la mecánica de fluidos. Ahora vamos a presentar otra herramienta, complemento de la anterior, con la cual seremos capaces de completar el aparato matemática necesario para plantear las ecuaciones fundamentales del movimiento de los fluidos: el teorema del transporte de Reynolds.
¿Por qué nos hace falta algo con ese nombre tan rimbombante? Veréis, para plantear las ecuaciones generales necesitamos evaluar cómo cambian una serie de magnitudes encerradas en lo que llamaremos un volumen de control, es decir, una región del fluido en la que ponemos nuestra lupa para mirar lo que entra en él, lo que sale, y lo que cambia en su interior. Rápidamente nos damos cuenta de que, al contrario de lo que pasa en un sólido, la forma del volumen de control se distorsionará mucho con el tiempo, por lo que necesitamos realizar esos balances teniendo a mano una herramienta que nos permita evaluar la evolución de los parámetros de interés a medida que el propio volumen de control evoluciona con el tiempo. Eso es precisamente lo que nos permite el teorema del transporte de Reynolds. Veámoslo:
Llamemos a la región contenida en nuestro volumen de control en un instante cualquiera \Omega_c (t). La superficie frontera de nuestro volumen de control en ese mismo instante, que es cerrada, será \Sigma_c (t). Nuestro objetivo es evaluar cómo cambia con el tiempo una magnitud \phi en el interior de dicho volumen.
\frac{d}{dt} \int_{\Omega_c (t)} \phi(\boldsymbol{x},t) d\varpi
Para evaluar lo anterior, podemos optar por dos caminos:
  • Podemos sustituir la derivada como un límite, hacer un par de desarrollos en serie de Taylor truncada en la primera derivada y, finalmente, evaluar el límite de la forma usual. Esta es la forma rigurosa y formal de demostrar el teorema, pero tiene el inconveniente de que, entre tantos pasos intermedios, podemos perder de vista la física de lo que hay detrás.
  • O bien, para mantener la física delante de nuestros ojos, podemos proceder utilizando una “conjetura razonable” que nos llevará al mismo resultado, que es lo que vamos a hacer.
1.-  No es difícil darse cuenta de que la derivada de la integral que queremos calcular no es más que un caso general de la derivada sustancial. En efecto, la derivada de la integral es un balance aplicado a un volumen finito. Por su parte, la derivada sustancial es también un balance, pero aplicado sobre una partícula material, un punto. En el límite, una partícula material no es más que un volumen infinitamente pequeño. Por tanto, podemos tratar de reconstruir la integral a partir de la derivada, teniendo en cuenta que la mayor diferencia entre los volúmenes de control es que, mientras que en el punto material el volumen de control y la superficie que lo envuelve colapsan en la misma entidad geométrica (el propio punto), en el caso de la integral dicho colapso no se produce. Por tanto:
\frac{d}{dt} \int_{\Omega_c (t)} \phi(\boldsymbol{x},t) d\varpi \leftrightarrow \frac{D\phi}{Dt}
Donde, en la expresión anterior, d\varpi es el elemento diferencial del volumen sobre el que realizamos la integral.
2.-  La derivada sustancial tenía un primer término que era la aceleración local de la magnitud al evolucionar el tiempo. Esto es asimilable en la integral a calcular la variación de la magnitud dentro del volumen de control, independientemente del movimiento del volumen:
\int_{\Omega_c (t)} \frac {\partial \phi}{\partial t} d\varpi \leftrightarrow \frac {\partial \phi}{\partial t}
3.-  Debemos evaluar ahora la derivada convectiva. Si recordamos el significado de la derivada convectiva, lo que expresaba era el cambio en la propiedad cuando seguíamos a una partícula inmersa en el fluido. Ahora, en vez de una partícula, lo que tenemos es un volumen finito, por lo que podemos imaginar fácilmente que cuando el volumen de control se mueve en el fluido, el flujo atravesará su superficie. De este modo, cualquier magnitud transportada con el fluido atravesará también el volumen de control. Este razonamiento nos lleva a equiparar la derivada convectiva con una operación que, en el caso de un volumen de control finito, pueda medir cuánto de esa magnitud que nos interesa está entrando y saliendo del mismo. Y ese, precisamente, es el concepto de flujo a través de una superficie. En este momento, y para ayudar a la interpretación de este concepto, conviene que mostremos el teorema de la divergencia:
\int_{\Omega} \nabla \cdot \boldsymbol{\Phi} d\varpi = \int_{\Sigma} \boldsymbol{\Phi} \cdot d\boldsymbol{\sigma}
Que viene a decir que toda cantidad que surge o se consume, pues la divergencia equivale a una fuente o a un sumidero, según sea el signo que tenga, en el interior de un volumen, (miembro izquierdo de la igualdad), es igual a la cantidad que atraviesa la frontera de dicho volumen (segundo término). Esto se ve más claro en la imagen siguiente, donde V denota el volumen y S la superficie que delimita dicho volumen:
Figura6
El segundo término del teorema de la divergencia define precisamente el flujo de una magnitud a través de una superficie. A la hora de aplicar el teorema de la divergencia hay que notar que tanto la magnitud que está fluyendo como la superficie tienen carácter vectorial. En el caso de la superficie esto puede resultar chocante, pero para tratar una superficie de forma vectorial no tenemos más que definir un vector que tenga como módulo el valor de la superficie y, como dirección y sentido, los dados por la normal que apunta hacia fuera de la superficie: d\boldsymbol{\sigma} = \boldsymbol{n}d\sigma.

Una vez hecho este pequeño inciso, para volver al teorema del transporte de Reynolds nos queda definir la derivada convectiva en un volumen como un flujo a través de una superficie. Para ello, sólo debemos usar que una magnitud transportada en un fluido tiene carácter vectorial si nos damos cuenta de que, al ir inmersa en el fluido, es transportada por el campo de velocidades de este. Usando la notación anterior,
\boldsymbol{\Phi} = \phi \boldsymbol{v}
Por tanto, el término de la derivada convectiva en forma integral nos queda como sigue:
\int_{\Sigma_c (t)} \phi \boldsymbol{v} \cdot \boldsymbol{n} d \sigma \leftrightarrow \boldsymbol{v} \cdot \nabla \phi
El teorema del transporte de Reynolds, por tanto, toma la forma:
\frac{d}{dt} \int_{\Omega_c (t)} \phi d\varpi = \int_{\Omega_c (t)} \frac{\partial \phi}{\partial t} d\varpi + \int_{\Sigma_c (t)}\phi \boldsymbol{v}\cdot\boldsymbol{n}d\sigma
La versión del teorema del transporte de Reynolds que hemos obtenido, pese a todo, no corresponde al caso más general, sino que sólo podemos aplicarlo cuando la velocidad a la que se mueve el volumen de control coincide con la propia velocidad del fluido. Si existe un movimiento relativo entre volumen de control y fluido (recordemos que el volumen de control se establece de forma arbitraria, por lo que ya puestos también se le puede dar un movimiento arbitrario, más rápido o más lento que el del fluido), se demuestra que la expresión del teorema debe modificarse de la siguiente forma:
\frac{d}{dt} \int_{\Omega_c (t)} \phi d\varpi = \int_{\Omega_c (t)} \frac{\partial \phi}{\partial t} d\varpi \int_{\Sigma_c (t)}\phi (\boldsymbol{v}-\boldsymbol{v_c})\cdot\boldsymbol{n}d\sigma
Donde \boldsymbol{v} es la velocidad del fluido y \boldsymbol{v_c} es la velocidad del volumen de control.

Conservación en fluidos

En esta entrada hemos definido el concepto básico de fluido, así como un par de herramientas matemáticas básicas para poder plantear de forma teórica el estudio del movimiento de los fluidos. Para hacerlo, debemos tener en cuenta que, como siempre se hace en física, se buscan cantidades que se conserven con el tiempo, para ver cómo afecta dicha conservación global a las diferentes magnitudes y propiedades que pueden ser medidas. Al encuadrarse dentro de la física clásica, las ecuaciones de conservación básicas que estudia la mecánica de fluidos son:
  • Conservación de la masa.
  • Conservación de la cantidad de movimiento.
  • Conservación de la energía.
Continuaremos con el tema de los fluidos en próximas entradas.
Nos seguimos leyendo…

Publicado por en