Supongamos que  es una función para la cual existen
es una función para la cual existen 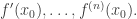
El polinomio de Taylor de grado  para
para  en
en  viene dado por
viene dado por
El resto de Taylor de orden  para
para  en
en  es la diferencia entre la función y su polinomio de Taylor, es decir,
es la diferencia entre la función y su polinomio de Taylor, es decir, 
La condición del resto asegura que
Suponiendo que existen 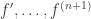 en un intervalo
en un intervalo  , el teorema de Taylor proporciona las siguientes expresiones para algún
, el teorema de Taylor proporciona las siguientes expresiones para algún 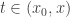
1. Cálculo de límites con expresiones indeterminadas
Una bonita aplicación de la condición del resto sucede al calcular el límite de una expresión indeterminada sustituyendo las funciones que aparecen por sus polinomios de Taylor.
Supongamos por ejemplo que queremos calcular
Tomando logaritmos y aplicando la regla de L’Hôpital resulta
Aplicando sucesivas veces la regla de L’Hôpital se obtienen expresiones cada vez más complicadas.
Un recurso es considerar polinomios de Taylor, digamos
donde los restos 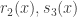 satisfacen las condiciones
satisfacen las condiciones 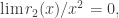
Tenemos
y esta expresión tiende hacia 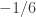 cuando
cuando 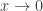 ,
,
de donde se deduce que
Se puede comprobar este resultado con Wolfram Alpha.
Al teclear el código
lim (sin(x)/x)^(1/x^2) as x goes to 0
se obtiene esta respuesta.
2. La base de los logaritmos naturales es un número irracional
Demostración.
Razonamos por reducción al absurdo.
Supongamos por un momento que 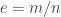 donde
donde 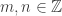 son números enteros con
son números enteros con 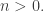
Considerando el polinomio de Taylor de grado  para la función exponencial
para la función exponencial
y particularizando esta expresión cuando 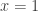 se obtiene
se obtiene
El resto de Lagrange viene dado por 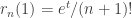 para algún
para algún  y por
y por
lo tanto 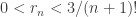
Multiplicando por 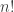 resulta
resulta
Los términos que aparecen en la expresión anterior son enteros pero