El principio de intervalos cerrados encajados de Cantor es otra expresión de la completitud del cuerpo de los números reales. Un sistema de intervalos encajados es cualquier familia de intervalos  con la propiedad de que para cada
con la propiedad de que para cada  se tiene
se tiene 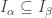 o bien
o bien 
| Teorema (Principio de intervalos encajados) Si |
Demostración.
Sea ![I_n = [a_n,b_n], I_n = [a_n,b_n],](http://s0.wp.com/latex.php?latex=I_n+%3D+%5Ba_n%2Cb_n%5D%2C&bg=ffffff&fg=333333&s=0) donde
donde  para cada
para cada  y sean
y sean 
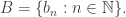 Está claro que
Está claro que  .
.
Como los intervalos están encajados, se tiene la desigualdad  para cada
para cada  y de aquí se deduce que
y de aquí se deduce que  está acotado superiormente y
está acotado superiormente y 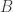 está acotado inferiormente.
está acotado inferiormente.
Ahora se sigue del axioma del supremo que existen 

Es fácil comprobar que entonces
y que bajo la hipótesis adicional se tiene 
Como ilustración del principio de intervalos encajados en acción tenemos una demostración alternativa del teorema de Bolzano acerca de la existencia de ceros para una función continua en un intervalo.
| Teorema de Bolzano Si |
Demostración.
Tomamos el punto medio 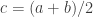 del intervalo
del intervalo ![[a,b]. [a,b].](http://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D.&bg=ffffff&fg=333333&s=0)
Si  entonces hemos concluido.
entonces hemos concluido.
Si  entonces elegimos
entonces elegimos 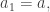
 , y si
, y si  entonces elegimos
entonces elegimos 
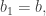 de modo que
de modo que 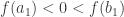 y
y 
Ahora tomamos el punto medio  del intervalo
del intervalo ![[a_1,b_1]. [a_1,b_1].](http://s0.wp.com/latex.php?latex=%5Ba_1%2Cb_1%5D.&bg=ffffff&fg=333333&s=0)
Si  entonces hemos concluido.
entonces hemos concluido.
Si  entonces elegimos
entonces elegimos 
 , y si
, y si  entonces elegimos
entonces elegimos 
 de modo que
de modo que  y
y 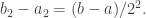
Continuando este proceso se obtiene una familia  de intervalos cerrados encajados
de intervalos cerrados encajados ![I_n=[a_n,b_n] I_n=[a_n,b_n]](http://s0.wp.com/latex.php?latex=I_n%3D%5Ba_n%2Cb_n%5D&bg=ffffff&fg=333333&s=0) tales que
tales que 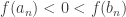 y
y 
Según el principio de intervalos encajados, existe algún número real
Afirmamos que  Supongamos lo contrario, digamos
Supongamos lo contrario, digamos 
Como  es continua en
es continua en  , existe
, existe 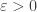 tal que
tal que  para cada
para cada 
Sea  tal que
tal que  Tenemos
Tenemos 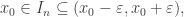 luego
luego 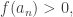 lo cual es absurdo.
lo cual es absurdo.
Cuando 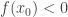 se razona de forma análoga.
se razona de forma análoga.