
El efecto túnel se usa para ilustrar la diferencia entre la mecánica clásica y la mecánica cuántica. Una partícula cuántica puede atravesar una barrera de potencial imposible de atravesar para una partícula clásica. Un fenómeno parajódico, en apariencia, cuando queremos localizar la partícula dentro de la barrera, o cuando queremos determinar la energía de la partícula mientras está dentro de la barrera. El principio de indeterminación de Heisenberg garantiza que la paradoja no existe. Al observar la partícula en la región donde se encuentra la barrera se obtendrá un valor de la energía superior a la de la barrera de potencial.
Muchos libros de texto discuten este problema. Por ejemplo, la sección 97, “The apparent paradox of the ‘tunnel effect’” en las páginas 334-335 del libro de D. I. Blokhinstsev, “Quantum Mechanics,” Reidel, 1964. Sin embargo, hay algunos físicos que aún no lo tienen del todo claro.
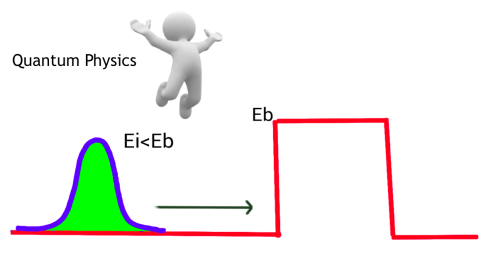
La función de onda cuántica Ψ(x) describe la probabilidad |Ψ(x)|² de la localizar la partícula con masa m y enegía Ei en la posición x.
La barrera de potencial con altura Eb>Ei tiene una anchura d (supongamos que la barrera está en 00 para x>d.
La probabilidad de atravesar la barrera es muy pequeña. Omito el cálculo matemático de los coeficientes de reflexión R y transmisión T, tales que R+T=1. El resultado es que el coeficiente de transmisión T ~ exp(–2 √(2m(Eb–Ei))d/ℏ) > 0, cuando la mecánica clásica predice T=0 para Eb>Ei. Por supuesto, el efecto túnel es observable sólo cuando T no es despreciable, o sea, cuando 2 √(2m(Eb–Ei))d/ℏ ~ 1. Para un electrón y una diferencia de potencial Eb–Ei ~ 10 eV se requiere d ~ 10–10 m = 0,1 nm para T ~ 1/e ~ 1/3.
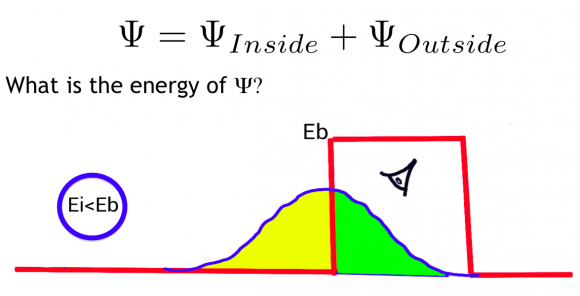
En mecánica cuántica la energía Ei de la partícula se puede separar en energía cinética Ek y energía potencial U, siendo Ei = Ek + U.
¿Qué energía tiene la partícula en la barrera de potencial? “tras darle un par de vueltas tendríamos que concluir, o al menos eso creo yo, que la energía es Eb.”
Algún lector puede pensar que como para 0Ei, entonces Ek<0 a="" aclaran="" algo="" arad="" cin="" como="" conclusi="" de="" decir="" energ="" es="" esta="" i="" imaginario="" imposible="" incorrecta.="" jico="" la="" libros="" lineal="" magnitud="" momento="" muchos="" n="" negativa.="" no="" o="" puede="" pues="" puro.="" real="" texto="" tica="" tomar="" un="" una="" valor="" velocidad="" y="">
La solución es el principio de indeterminación de Heisenberg, Δx Δp ≥ ℏ. Recuerda que la posición media de la partícula viene dada por
Δx = x – , con <Δx>=0 y varianza <Δx²> = – ² (la desviación típica es igual a la raíz cuadrada de la varianza, es decir, σ(x) = √<Δx²>).
Y lo mismo para el momento, lo que implica que las varianzas estadísticas en la medida reiterada de dichas magnitudes cumple <Δx²><Δp²> ≥ ℏ²/4 (expresión fácil de derivar). Como localizar la partícula en la región de la barrera de potencial requiere que Δx < d, tenemos que Δp ≥ ℏ/d.
Por tanto, la varianza del momento <Δp²> ≥ ℏ²/(4 <Δx²>) > ℏ²/(4 d²).
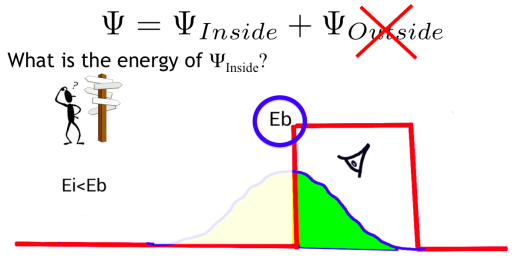
La fórmula Ei = Ek(p) + U(x) asume la determinación simultánea de la posición, U(x), y de la velocidad, Ek(p) = p²/(2m). Ya hemos dicho que el efecto túnel es observable cuando 2 √(2m(Eb–Ei))d/ℏ ~ 1, es decir, 2 √(2m(Eb–Ei)) ~ ℏ/d. Por tanto, tenemos que <Δp²>/(2m) ≥ Eb–Ei, es decir, el cambio en la energía cinética de la partícula durante el proceso de medida es mayor que la diferencia entre la energía de la partícula y la altura de la barrera de potencial.
Como en mecánica cuántica el proceso de medida altera las propiedades del objeto medido. La medida de la partícula que conduzca a su localización espacial en la región de la barrera de potencial implica tal cambio en su energía cinética que su energía total Ei>Eb.
Toda partícula que se observe en la región de la barrera tendrá una energía total superior a la propia barrera. Sólo es posible observar una partícula con una energía total menor que la barrera a ambos lados (o bien x<0 bien="" o="" x="">d).

Imagina que quieres ver la partícula en la barrera de potencial usando fotones (haces de luz láser). Para localizar la partícula en una región de tamaño Δx tendrás que usar fotones con una longitud de onda λ < Δx.
Para localizar la partícula en la barrera tendrás que usar fotones con λ < d/2 ~ ℏ/√(2m(Eb–Ei)). Elevando al cuadrado e introduciendo la frecuencia, λ=c/ν, tenemos ℏ²ν² > 2 m c² (Eb–Ei).
Estamos usando mecánica cuántica no relativista, es decir, fotones con energía insuficiente para crear un par partícula-antipartícula, es decir, ℏν < 2 m c². Por tanto, el fotón debe tener una energía ℏν > Eb–Ei, es decir, para localizar la partícula en la región de la barrera tengo que usar un fotón que le cede una energía suficiente para que adquiera una energía total por encima de la barrera.
En la región de la barrera de potencial es imposible localizar una partícula con una energía total menor que su altura.
En resumen, el principio de indeterminación de Heisenberg garantiza que cualquier intento de localizar la partícula en la región de la barrera requiere dotar a la partícula de una energía superior a la propia barrera.
Sólo puedo localizar la partícula con una energía total menor que la altura de la barrera a ambos lados de la barrera.
La paradoja del efecto túnel es solo aparente.
http://francis.naukas.com/