
Rumor confirmado. La anomalía observada por LHCb en los ángulos de los productos de la desintegración B0→K*0μ+μ–, con K*0→K+π–, no ha desaparecido tras analizar 3 /fb de colisiones. Sin embargo, la significación estadística no ha crecido y sigue siendo 3,7 sigmas (para el parámetro P’5), igual que tras analizar 1 /fb de colisiones en 2013. Que no haya variado la significación implica que su origen no es estadístico, luego podría ser sistemático. La hipótesis más conservadora es asumir que no se está calculando bien la predicción del modelo estándar. Un efecto hadrónico podría ser la causa (al final de esta entrada lo explico para legos en la materia).
En la figura que abre esta entrada, el resultado más anómalo, asociado a la variable angular llamada P’5, se observa con 2,9 sigmas en los intervalos [4,6] y [6,8] GeV², que combinados implican 3,7 sigmas al 95% CL en los puntos negros con barras de error tras analizar 3 /fb de colisiones. Este resultado se compara con el resultado tras analizar 1 /fb en los puntos azules con barras de error. La predicción del modelo estándar (sin tener en cuenta ningún efecto hadrónico) está representada por los rectángulos naranja. Se observa que la anomalía persiste, pero no se hace más significativa .
Recomiendo consultar las transparencias de la charla de Christoph Langenbruch, “Latest results on rare decays from LHCb,” 50th Rencontres de Moriond Electroweak, in La Thuile (Italy), 20 Mar 2015 [slides PDF]. También las explicaciones teóricas más allá del modelo estándar de Joaquim Matias, “B to K(*)mu+mu-: theory interpretation,” 50 Moriond EW, 20 Mar 2015 [slides PDF], y dentro del modelo estándar de David Straub, “Implications of b→s measurements for model-building,” 50 Moriond EW, 20 Mar 2015 [slides PDF]; un resumen de este último en David Straub, “The B→K*μμ anomaly persists,” Blog personal, 20 Mar 2015.
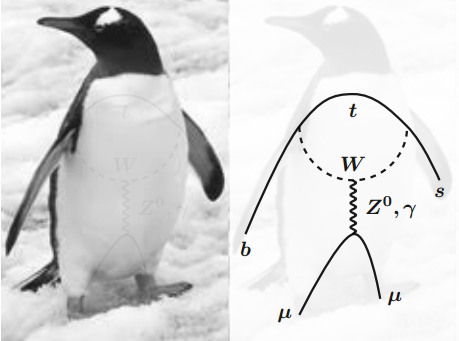
En el modelo estándar la desintegración B→K*μμ está asociada a un diagrama de Feynman de tipo pingüino para la desintegración de un quark bottom en un quark strange(o down), vía un bucle que involucra una corriente neutra; o bien un quark top y un bosón W que emite un bosón Z (o un fotón) que se desintegra en un par de leptones, o bien un bosón W y un quark top que emite un bosón Z (o un fotón) que se desintegra en un par de leptones; por supuesto, también se dan los diagramas correspondientes a intercambiar partículas y antipartículas. Estos diagramas están fuertemente suprimidos en el modelo estándar y por ello se trata de modos raros (poco probables) de desintegración de un hadrón B (tanto mesón B como barión Λb).

La tasa de desintegración (branching ratio) del proceso B→K*μμ coincide con la predicción del modelo estándar, como han confirmado LHCb, Belle, BaBar y otros detectores. Sin embargo, en el año 2013 se acometió un curioso estudio de los ángulos de salida de los productos de la desintegración (los dos muones y los dos mesones, pión y kaón).
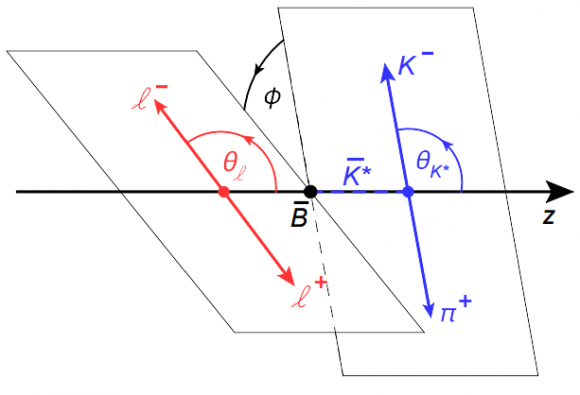
Por las leyes de conservación del momento los dos muones aparecen en un plano con cierto ángulo respecto a la dirección del mesón B (sea θl), los dos mesones aparecen en otro plano con un segundo ángulo (sea θK*) y entre ambos planos habrá un tercer ángulo (sea ϕ). En el modelo estándar (QCD) estos tres ángulos dependen de ocho parámetros del lagrangiano a baja energía llamados FL, AFB, S4, S5, …, S9. En LHCb ha observado la anomalía al estudiar las combinaciones P’4,5 = S4,5/√(FL (1−FL)), sobre todo en P’5 (ver figura que abre esta entrada). Omito todos los detalles técnicos (que sólo tiene interés para quien ya conoce estos detalles). Pero no me resisto a destacar que la predicción del modelo estándar para esta anomalía es muy difícil de calcular con precisión porque depende de ocho parámetros.
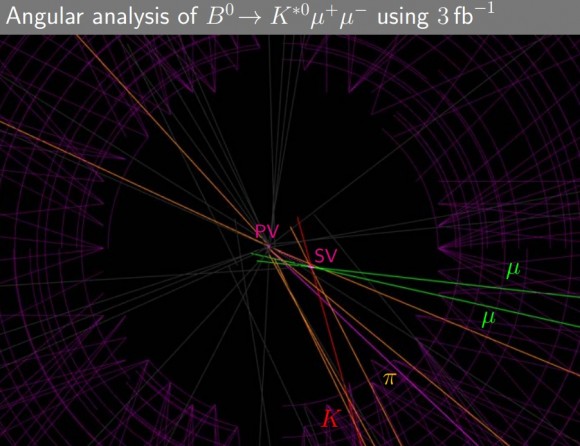
¿Qué explicación puede tener la anomalía observada por LHCb? Obviamente, todo el mundo desea que se trate de física más allá del modelo estándar. Matias en su charla apunta a un bosón Z’, pero hay muchas otras. Sin embargo, Straub apunta a una explicación más prosaica, no se ha calculado bien la predicción del modelo estándar. ¿Por qué? Por la presencia de los leptones (muones en este caso) durante la hadronización de los productos. Efectos QED que no se han tenido en cuenta en el cálculo QCD. No es fácil realizar estos cálculos. Por ello la sugerencia de Straub no es la explicación definitiva. Pero ya se sabe que afirmaciones extraordinarias (nueva física) requieren evidencias extraordinarias (más fuertes que una simple anomalía). A petición, trataré de explicar sin usar términos muy técnicos cuál es la explicación propuesta por Straub.
La cromodinámica cuántica (QCD) es una teoría mucho más complicada que la electrodinámica cuántica (QED). Explica la interacción entre los quarks (los únicos fermiones con carga de color) mediada por ocho gluones de manera similar a la interacción entre fermiones cargados (quarks y leptones) mediada por fotones. Sin embargo, se diferencia por la libertad asintótica, la fuerza de color entre quarks aumenta con la distancia en lugar de disminuir, y por el confinamiento, todos los quarks se hadronizan formando partículas compuestas neutras para la carga de color (bariones y mesones).
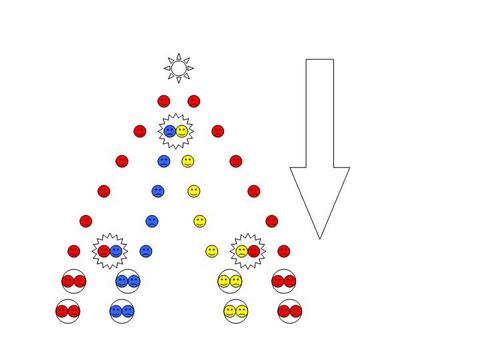
La hadronización es un fenómeno muy rápido (en la escala de los yoctosegundos, 10–24 s) que sufren todos los quarks (excepto el quark top cuya vida media es de unos 0,5 yoctosegundos). Esta figura de Tommaso Dorigo muestra la desintegración de un bosón Z en un par quark-antiquark (rojos) que se hadronizan formando un rosario de cuatro mesones. El quark y el antiquark excitan el vacío del campo de gluones y aparecen a su alrededor gran número de gluones virtuales de alta energía. Estos gluones virtuales se desintegran en pares quark-antiquark virtuales. Uno de estos pares virtuales se transforma en un par real (no virtual) que se acopla a la pareja de quarks originales formando un par de mesones. En las colisiones de alta energía este proceso ocurre varias veces hasta que los mesones resultantes están suficientemente alejados entre sí para que el campo de color entre ellos sea despreciable. En la hadronización, en pocos yoctosegundos, todo quark (antiquark) queda revestido por un campo de gluones y pares quark-antiquark virtuales formando un mesón (o un barión).

La imagen naïve es que un mesón está formado por un quark y un antiquark (llamados de valencia). Y que un barión está formado por tres quarks de diferente color. Sin embargo, habrás oído que la masa de un protón es cien veces mayor que la masa de sus tres quarks de valencia; lo mismo le pasa a todos los hadrones. Un protón está formado por infinidad de gluones virtuales de alta energía (unas cincuenta veces mayor que la masa de un quark), que producen infinidad de pares quark-antiquark virtuales. En cierto sentido un protón es como una gota de agua y está formado por un mar de quarks, antiquarks y gluones. A más energía, más complicado es un protón. Lo mismo le ocurre a los mesones B.
En los cálculos de las predicciones del modelo estándar para los mesones B se asume que toda la complejidad de un mesón se reduce a un factor de forma (una relación entre la energía promedio y el momento promedio de todos sus constituyentes). Cuando se calculan los ángulos de salida de los productos en la desintegración B0→K*0μ+μ–→K+π–μ+μ–, se asume que un quark bottom se desintegra en uno strange mediante un diagrama de pingüino de tipo b→s μ+μ–, modelando toda la complejidad hadrónica de estos mesones usando el correspondiente factor de forma. Una simplificación necesaria para un cálculo que de otra manera sería casi imposible de realizar.

El efecto hadrónico que propone Straub consiste en considerar que la hadronización influye en el vértice b→s μ+μ–, es decir, que no es un vértice tipo pingüino limpio, sino que hay pares virtuales quark-antiquark (tipo charm, por ejemplo) que influyen en este vértice alterando de forma efectiva los ángulos de salida de los leptones (muones en este caso).
El cálculo de este efecto hadrónico es muy complicado y Straub no es capaz de realizarlo. Si su intuición es correcta este efecto sería independiente de la energía asociada al factor de forma del mesón.

Para apoyar su hipótesis, Straub compara los resultados experimentales de LHCb para un coeficiente técnico llamado coeficiente de Wilson C9. No quiero entrar en detalles técnicos, pero la existencia de nueva física implica que este coeficiente depende fuertemente de la energía. Los nuevos resultados de LHCb apuntan a que este coeficiente no depende de la energía (la incertidumbre es grande, pero Straub afirma que es constante con una sigma de significación estadística). Por tanto, en su opinión, un efecto hadrónico podría explicar dentro del modelo estándar la anomalía observada por LHCb.
Estimado lector, si has llegado a este punto quizás necesites una aclaración para legos sobre este asunto.
Permíteme abusar del lenguaje y de las analogías físicas por un momento.
Un mesón B es parecido a una gota de un líquido polar (como el agua).
Los ángulos de los productos de su desintegración dependen de la forma esta gota.
Las predicciones del modelo estándar usadas por LHCb se basan en asumir que la gota es esférica. La idea de Straub es que la presencia de los leptones (muones) entre los productos de desintegración produce una atracción electromagnética a la gota polar que la deforma.
Llama a este efecto hadrónico porque ocurre durante la hadronización de los productos, pero no es un efecto QCD puro que se pueda incorporar como un cambio en el factor de forma.
Como resultado el mesón B se comporta como una gota alargada y los ángulos de salida de los productos difieren de las predicciones para una gota esférica. Sin embargo, la tasa de desintegración no se ve afectada, pues no depende de la forma de la gota. He forzado un poco la analogía, pero espero que aclare un poco el asunto.
En resumen, la anomalía observada por LHCb dará que hablar bastante en los próximos años, pero bien podría ser resultado de un cálculo incorrecto de la predicción teórica para los ángulos de salida de los productos.
Tanto si su origen es nueva física, como si se trata de un efecto de alto orden en el modelo estándar, gracias a esta anomalía aprenderemos muchas cosas sobre la física de los mesones B. Al fin y al cabo de ese se trata, de entender cada vez mejor la Naturaleza de nuestro universo.
http://francis.naukas.com/