viernes, 3 de julio de 2015

Café matemático: El criterio de condensación


El criterio de condensación de Cauchy asegura que si 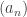(a_n) es una sucesión decreciente de números reales positivos entonces la serie infinita 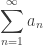\displaystyle{\sum_{n=1}^\infty a_n} tiene el mismo carácter que la serie condensada \displaystyle{\sum_{k=0}^\infty 2^k a_{2^k}.}
Consideremos por ejemplo la serie infinita
\displaystyle{\sum_{n=2}^\infty \frac{1}{(\log n)^{\log n}}}.
Es evidente que la sucesión 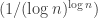(1/(\log n)^{\log n}) es decreciente y que sus términos son positivos. Se sigue del criterio de condensación de Cauchy que esta serie infinita tiene el mismo carácter que la serie condensada
\displaystyle{\sum_{k=1}^\infty \frac{2^k}{(\log (2^k))^{\log (2^k)}}= \sum_{k=1}^\infty \frac{2^k}{(k \log 2)^{k \log 2}}}.
Si aplicamos el criterio de la raíz a la nueva serie resulta
\displaystyle{\lim_{k \to \infty} \sqrt[k]{\frac{2^k}{(k \log 2)^{k \log 2}}}= \lim_{k \to \infty} \frac{2}{(k \log 2)^{\log 2}} =0}
y por lo tanto la serie es convergente.
Publicado por en