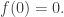Primer problema
- Calcular la integral impropia
- Demostrar que la integral impropia
es convergente.
- Utilizar el cambio de variable
para probar que
- Calcular la integral impropia
Solución
Aplicando la fórmula de integración por partes con el esquema  resulta
resulta  luego
luego ![\displaystyle{\int_0^1 \log x\, dx= \lim_{\varepsilon \rightarrow 0+} \int_\varepsilon^1 \log x\, dx= \lim_{\varepsilon \rightarrow 0+} [-\varepsilon \log \varepsilon -(1-\varepsilon)]=-1.} \displaystyle{\int_0^1 \log x\, dx= \lim_{\varepsilon \rightarrow 0+} \int_\varepsilon^1 \log x\, dx= \lim_{\varepsilon \rightarrow 0+} [-\varepsilon \log \varepsilon -(1-\varepsilon)]=-1.}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B%5Cint_0%5E1+%5Clog+x%5C%2C+dx%3D+%5Clim_%7B%5Cvarepsilon+%5Crightarrow+0%2B%7D+%5Cint_%5Cvarepsilon%5E1+%5Clog+x%5C%2C+dx%3D+%5Clim_%7B%5Cvarepsilon+%5Crightarrow+0%2B%7D+%5B-%5Cvarepsilon+%5Clog+%5Cvarepsilon+-%281-%5Cvarepsilon%29%5D%3D-1.%7D&bg=ffffff&fg=333333&s=0)
El segundo apartado parece deducirse fácilmente del criterio de comparación directa, porque 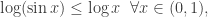 pero esto es un error, porque ambas funciones son negativas en el intervalo
pero esto es un error, porque ambas funciones son negativas en el intervalo 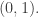
Sin embargo, 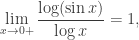 y entonces el criterio de comparación asintótica viene al rescate para concluir que
y entonces el criterio de comparación asintótica viene al rescate para concluir que 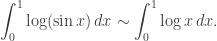
El tercer apartado se resuelve practicando el cambio de variable 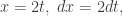 de tal modo que
de tal modo que  y por lo tanto
y por lo tanto
como queríamos demostrar.
Ahora observamos que, por razones de simetría,  de donde
de donde  y por lo tanto
y por lo tanto 
Segundo problema
- Probar que la serie de funciones
converge puntualmente en la recta real hacia una función
digamos.
- Demostrar que la convergencia es uniforme sobre el intervalo
donde
Indicación: Hallar primero el máximo de
sobre
- Demostrar que
para cada
y deducir que
Indicación: Estimar la suma mediante una integral impropia.
- Concluir que la serie de funciones no converge uniformemente en la recta real.
Solución
Si 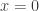 entonces todos los términos de la serie se anulan, y si
entonces todos los términos de la serie se anulan, y si  entonces se tiene
entonces se tiene
Ahora observamos que ![\displaystyle{\frac{d}{dx}\left [ \frac{nx}{1+n^4x^2} \right ]=\frac{n(1-n^4x^2)}{(1+n^4x^2)^2}=0} \displaystyle{\frac{d}{dx}\left [ \frac{nx}{1+n^4x^2} \right ]=\frac{n(1-n^4x^2)}{(1+n^4x^2)^2}=0}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B%5Cfrac%7Bd%7D%7Bdx%7D%5Cleft+%5B+%5Cfrac%7Bnx%7D%7B1%2Bn%5E4x%5E2%7D+%5Cright+%5D%3D%5Cfrac%7Bn%281-n%5E4x%5E2%29%7D%7B%281%2Bn%5E4x%5E2%29%5E2%7D%3D0%7D&bg=ffffff&fg=333333&s=0) cuando
cuando 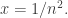
Sea  y sea
y sea 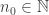 tal que
tal que 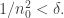
Sea 
Si 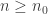 entonces
entonces 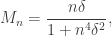 luego
luego 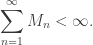
Se deduce de la prueba de mayoración de Weierstrass que la serie de funciones converge uniformemente en el intervalo 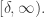
A continuación tenemos
Siguiendo la indicación, estimamos esta suma mediante una integral impropia, a saber,
de donde se deduce que 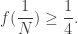
Finalmente concluimos que la serie de funciones no converge uniformemente sobre la recta real, porque siendo cada término una función continua, bajo el supuesto de convergencia uniforme 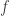 debe ser una función continua, luego
debe ser una función continua, luego 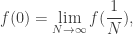 lo cual es una contradicción puesto que
lo cual es una contradicción puesto que