
La física teórica es una de las ramas del saber donde uno ve más claro que cuanto más sabe menos sabe. Uno puede preguntar a cualquier persona por la calle qué es el vacío y sin duda obtendrá respuestas contundentes como “un sitio donde no hay nada”. Sin embargo, en mecánica cuántica la cosa se complica enormemente. Sobre todo en mecánica cuántica no inercial.
En el siglo XVII, los tiempos de Newton, lo más complicado era resolver el problema de tres cuerpos moviéndose en conjunto con espacio vacío entre ellos. Con la llegada de la relatividad de Einstein a principios del siglo XX y los distintos sistemas de referencia, el movimiento de dos cuerpos pasó a ser también muy complicado si se quería hacer con precisión.
Poco después, en la década de los veinte, la mecánica cuántica dificultaría el análisis del movimiento de una sola partícula.
Finalmente, con la teoría cuántica de campos, el propio vacío da problemas.
En esta entrada comenzaremos a adentrarnos en el mundo de la teoría cuántica de campos y la segunda cuantización y veremos que, contra toda intuición (en principio) lo que un observador dice que está vacío otro puede opinar que tiene partículas. Este intrigante hecho supuso el comienzo de “la guerra de los agujeros negros” en la guerra de los setenta y ha llevado a desarrollar las teorías más potentes de las que disponemos de gravedad cuántica.
No obstante, no ahondaremos en eso hasta entradas posteriores.
Repasando el campo de probabilidad de Schrödinger:
El campo de Schrödinger ψ con masa m venía dado por la siguiente lagrangiana y ecuaciones de movimiento:
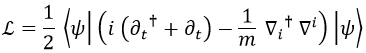
En esta ocasión estoy usando la notación ∇ para derivadas espaciales porque nos vamos a salir de geometría de Minkowski en breves momentos.
A partir de esta lagrangiana, el campo debía cumplir las ecuaciones de Euler-Lagrange:

Lo que llevaba inmediatamente a la ecuación de Schrödinger:
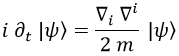
Aquí se cumplía la relación cuántica entre el cuadrimomento y la cuadriderivada:
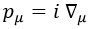
Lo que nos permitía identificar la ecuación de Schrödinger para un campo libre con la ecuación de la energía cinética clásica:
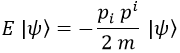
Esta ecuación diferencial para obtener campos cuánticos de probabilidad evidentemente no podía ser general, dado que no es acorde con los postulados de la teoría de la relatividad. ¿Qué impide en la ecuación de Schrödinger a un campo tener mayor velocidad que la de la luz? Absolutamente nada.
El propio Schrödinger era consciente de esto cuando desarrolló su modelo y de hecho parece ser que llegó a la ecuación relativista adecuada, pero sin embargo se le conoce por su versión clásica.
El campo relativista de probabilidad de Klein-Gordon:
En la lagrangiana de Schrödinger tiempo y espacio son entidades completamente ajenas la una a la otra. Esto, además de ser feo, implica que de ningún modo puede ser relativista. Un tratamiento adecuado tendría que pasar por unificar tiempo y espacio, y eso se consigue fácilmente haciendo intervenir a cuadriderivadas en vez de usar derivadas temporales por un lado y espaciales por el otro.
La lagrangiana comúnmente empleada es esta:
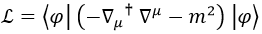
La mejor forma de justificarla es hacer cuentas con ella, así que vamos directos al grano. Si calculamos la primera parte de la ecuación de Euler-Lagrange asociada obtenemos:
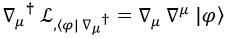
Aquí hemos tenido en cuenta que la derivada adjunta es igual a la derivada habitual cambiando de signo.
La segunda parte de la ecuación da:
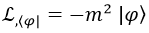
Igualando ambas obtenemos la ecuación de Klein-Gordon:
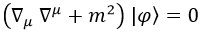
Y sustituyendo por cuadrimomentos se llega a nada más y nada menos que la ecuación de masa de la relatividad especial:
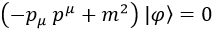
El término entre paréntesis siempre, por definición, va a ser nulo. Pero recordemos que lo que buscamos es una ecuación diferencial que nos permita despejar el campo, que es lo que tenemos arriba.
El campo escalar sin masa:
En la ecuación de Schrödinger es inviable que un campo de probabilidad no tenga masa. Sin embargo, en el caso de Klein-Gordon no pasa absolutamente nada relevante si nos la cargamos. La ecuación diferencial entonces pasa a ser:
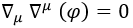
Y esto tiene dos posibles soluciones con la única condición de que el módulo del cuadrimomento sea nulo:
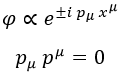
Un campo escalar sin masa no existe en el modelo estándar de la física de partículas. Sin embargo, como campo de juguete para hacer cuentas que con otros campos más complicados se hacen cuesta arriba es muy útil.
La segunda cuantización:
Como vimos en la entrada de energía nuclear, el hecho de que en relatividad masa fuese igual a energía implicaba que el teorema de conservación de la masa dejase de ser cierto, en tanto que esta puede deshacerse y crearse.
Consecuentemente, en la teoría de campos cuánticos relativistas el número de partículas involucradas en un sistema no es constante.
De hecho, las partículas serán generadas y destruidas por sus campos asociados. Así, el campo escalar sin masa visto antes generaría partículas sin espín ni masa moviéndose a la velocidad de la luz y el campo electromagnético generaría fotones con espín.
¿Y cómo expresamos que un campo cuántico es un generador/destructor de partículas?
Pues teniendo en cuenta que las partículas se propagan como ondas y la teoría de operadores de creación y destrucción ya mencionada en su momento.
Supongamos que tenemos n partículas oscilando con una frecuencia ω. Denominaremos a ese estado del espacio por nω. Si sobre este estado hacemos actuar un operador de destrucción aω nos cargaremos una de las partículas:

Por el contrario, si hacemos actuar sobre el estado un operador de creación aparecerá una partícula:
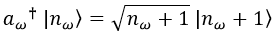
El operador de destrucción actuando sobre el estado 0 destruye el estado, y el de creación sobre el vacío adjunto también:
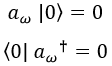
Cabe destacar que cada campo tiene sus propios operadores de creación y destrucción asociados, en cuya forma analítica no nos metemos.
Para contar el número de partículas en un estado concreto recurríamos al operador número N:
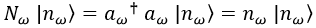
Si, por otra parte, quisiésemos saber el número de partículas elevado en 1, podríamos hacer la siguiente cuenta:
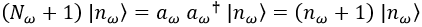
Teniendo todo esto en mente, podemos identificar el campo escalar puesto como ejemplo con un operador que cree y destruya ondas de distintas frecuencias en todas direcciones.
Si nos restringimos al eje x podríamos expresarlo así:
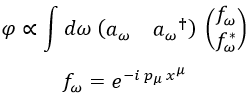
Es importante que la dirección de propagación de las ondas vinculadas al operador de creación sean opuestas al de destrucción (complejo conjugado) para que en efecto uno cancele el otro.
El signo concreto que se asocie en el exponente a cada una en realidad es bastante irrelevante, en tanto que podemos invertir el eje x sin problema y estaríamos analizando lo mismo.
Esta expresión de un campo como conjunto de operadores se conoce como la segunda cuantización, dado que volvemos discreto algo que antes era continuo: el propio campo.
Distintos vacíos:
En la sección anterior hemos expresado un campo mediante su expansión en serie de operadores de creación y destrucción.
Estos operadores deben ser acordes a las funciones de onda fω que se obtengan de la ecuación diferencial del campo.
En teoría cuántica de campos usual las ecuaciones de estos son 100% relativistas, lo que implica que son invariantes frente a giros espaciales de las coordenadas, desplazamientos y rotaciones espacio-temporales (transformaciones de Lorentz).
Por tanto, la exponencial compleja usual siempre será solución para cualquier observador.
Sin embargo, si aceptamos la posibilidad de que el espacio-tiempo esté curvado la ecuación diferencial se ve afectada por la geometría y sus soluciones no serán las mismas que en el caso minkowskiano:
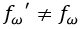
Denominaremos con primas las distintas formas de propagarse que se podrían obtener en un espacio-tiempo curvado genérico.
Podemos definir los coeficientes α y β que relacionan una función nueva f’ω’ con una anterior fω y su dual haciendo el producto escalar entre ambas:
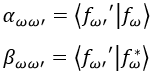
Sabiendo esto, podemos expandir las funciones f’ω’ y sus conjugadas del siguiente modo:
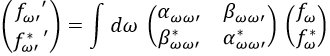
La ecuación que quedaría en la segunda fila es, como no podría ser de otro modo, la conjugada de la primera fila.
Dado que buscaremos normalizar todas las funciones de forma que la probabilidad, el módulo del campo, se conserve, es necesario que siempre se cumpla que el determinante de la matriz de coeficientes sea 1 al ser integrado, lo que lleva a la relación:

Y sabiendo esto la transformación se puede invertir fácilmente sin más que recurrir a la matriz inversa:
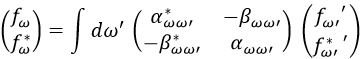
Y si las funciones fω transforman de este modo, el principio de covarianza exige que los operadores de creación y destrucción se transformen también y de forma opuesta. De otro modo, el campo escalar no sería un invariante relativista:
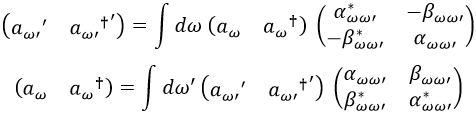
Gracias a esta transformación podemos deducir de forma sencilla que el campo escalar tiene la misma expresión en el sistema de coordenadas curvado y en el no curvado:
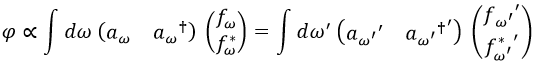
Dado que las funciones fω son diferentes en cada sistema y no se pueden relacionar una a una, hay que considerar que a priori los vacíos de cada uno, es decir, los estados 0, pueden ser diferentes.
El valor medio del operador número en ambos sistemas cuando tenemos el vacío de cada uno de ellos será nulo por construcción:
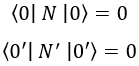
Sin embargo, si aplicamos el operador número del sistema habitual al vacío del sistema curvado obtenemos una cantidad de partículas no nula:
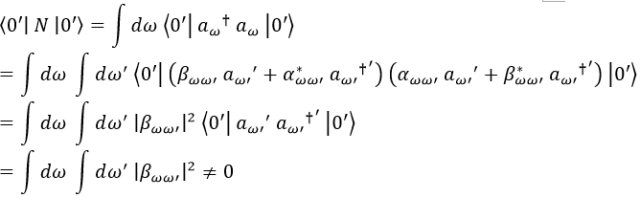
Así pues, donde un observador puede opinar que hay vacío otro puede ver partículas bajo la única condición de que el movimiento relativo entre ambos no sea una de las transformaciones básicas de la mecánica: rotaciones, desplazamientos o giros de Lorentz.
La aparición de fuerzas implica la aparición de partículas observadas, como la intuición ya podría anticipar.
El efecto Unruh:
Veamos para concluir un ejemplo sencillo de cálculo de por qué las fuerzas y aceleraciones implican partículas nuevas.
Pongamos por caso que observamos un cuerpo en reposo con nosotros empezar a moverse con aceleración uniforme a. La rapidez φ de su desplazamiento será su aceleración por el tiempo propio τ de ambos:
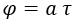
La rapidez, por su parte, se relaciona con la velocidad observada v mediante una tangente hiperbólica:
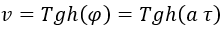
Ahora supongamos que tenemos una partícula de un campo propagándose con esta aceleración. Su frecuencia como ondaω0 padecerá un efecto Doppler dependiente del tiempo que se puede obtener de la ecuación del efecto Doppler relativista:
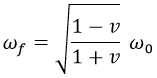
El término de la raíz se puede simplificar haciendo algunos apaños:
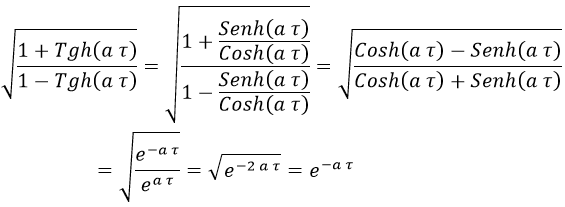
Con lo cual, tenemos un efecto Doppler tal que:
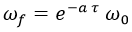
A medida que pasa el tiempo, la frecuencia observada se vuelve prácticamente nula si una partícula se aleja de nosotros aceleradamente.
Su fase, que sería la integral de su frecuencia base por el tiempo obviando la parte espacial, evolucionaría del siguiente modo:
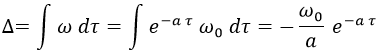
Esto nos dejaría una función de onda del siguiente modo:
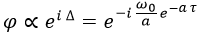
El módulo cuadrado de esta función daría la probabilidad de encontrar la partícula en un tiempo dado, pero eso no nos sería útil apenas.
Es mucho más interesante realizar una transformada de Fourier para obtener la función de onda en función de onda en función de la energía Ω:
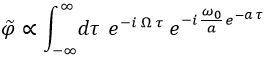
Esta integral se puede retocar un poco mediante el siguiente cambio de variable:
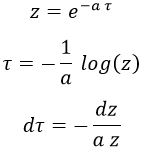
Teniendo esto en cuenta la integral queda como:

La cual está tabulada del siguiente modo:
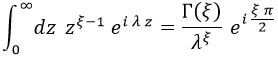
Aquí Γ es la función gamma de Euler, tabulada también.
En suma, tenemos:
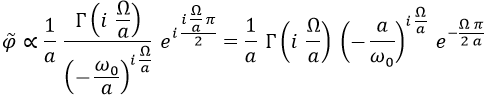
Cuyo módulo cuadrado es:
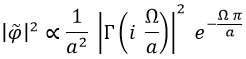
El módulo cuadrado de la gamma de Euler en ese caso también está tabulado y sería:
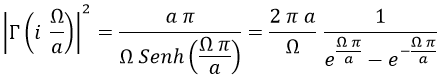
Con lo que, sustituyendo, finalmente tenemos que la probabilidad de encontrar el campo con una energía Ω es:
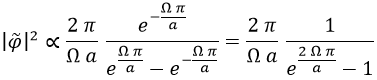
Esto recuerda de forma muy sospechosa a la probabilidad de encontrar una partícula bosónica con energía Ω vista en mecánica estadística. En efecto, nuestro campo escalar es bosónico dado que nada impide que genere montones de partículas idénticas en el mismo estado.
Así pues, surge de forma natural la relación entre su probabilidad y la de un sistema de bosones a temperatura T:
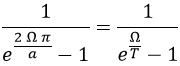
Es decir, que cuando observamos un campo con movimiento acelerado es prácticamente como si lo observásemos con una temperatura proporcional a la aceleración observada en tiempo propio:
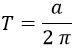
Así pues, lo que pare un observador es vacío para otro puede ser un sistema térmico con una temperatura de esta forma. Esta dualidad se conoce como efecto Unruh y su principal consecuencia es la radiación de Hawking de los agujeros negros, que comentaremos en la siguiente entrada.
Pero ante todo, el efecto Unruh tiene una implicación intrigante:
¿lo que nosotros vemos como vacío… no lo es para algún otro observador?
¿Estamos en un sistema de referencia no privilegiado?
La cosmología estándar nos dice que en principio, dado que todas las regiones del universo son equivalentes, en principio nuestro vacío es el vacío correcto y el único en el que tiene sentido pensar.
Para aquellos interesados en esta derivación del efecto Unruh, que no es la habitual y la he aprovechado para introducirlo sin meterme de lleno en el asunto, el artículo original donde la comentaron es
si bien consideraron la aceleración con el signo cambiado.
No obstante ese detalle es irrelevante y da el mismo resultado.