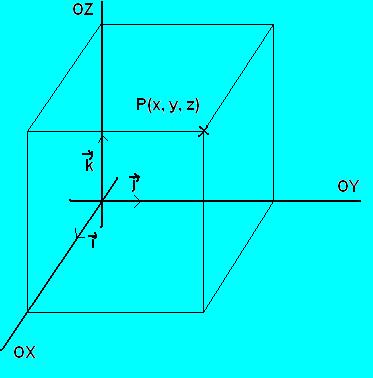
Consideremos tres rectas “x”, “y”, “z”, que son mutuamente perpendiculares y se intersecan en un mismo punto “O“. Éste punto se denominará origen de coordenadas y divide a cada eje en dos semiejes (positivo y negativo). Para cada punto “M” del espacio podemos encontrar las correspondientes coordenadas “P“, “Q“, “R“, de la siguiente forma.
El punto “P” es la intersección del eje “OX” con un eje paralelo al plano “yz” que pasa por “M“. De modo análogo se obtienen los puntos “Q” y “R” como resultado de la proyección del punto “M” en sus respectivos ejes coordenados.
La longitud de los segmentos es:
- OP = x.
- OQ = y.
- OR = z.
, de modo que a cada punto del espacio le asignaremos la terna ordenada de números (x, y, z).
Denotaremos por “i“, “j“, “k“, a los vectores unitarios coordenados cuya dirección y sentido es el positivo de estos ejes. Dado un punto arbitrario “M“, se cumple que su vector de posición satisface
- OM = OP + OQ + OR.
En términos de los vectores unitarios:
- OM = x i + y j + z k.
Siendo siempre:
- x = OM i.
- y = OM j.
- z = OM k.
La base (i, j, k) del espacio tridimensional es una base ortonormal, ya que todos sus vectores son unitarios y ortogonales dos a dos. Existe correspondencia biunívoca (única) entre cada punto “M” del espacio y el conjunto de las coordenadas cartesianas rectangulares (x, y, z).
Distancia entre Dos Puntos:
Sean los puntos “M1” y “M2“, y sean sus coordenadas respectivas (x1, y1, z1) y (x2, y2, z2). Denominaremos distancia entre los puntos “M1” y “M2” a la longitud del segmento que los une:
- d(M1, M2) = [(x1 – x2)^2 + (y1 – y2)^2 + (z1 – z2)^2]^1/2.
Este resultado se obtiene aplicando reiteradamente el Teorema de Pitágoras. A esta distancia se le denomina distancia mínima euclídea entre los puntos “M1” y “M2“.
Transformación de Coordenadas:
Consideremos dos sistemas de ejes de coordenadas cartesianos (x, y, z) y (x’, y’, z’), con sus respectivos orígenes “O” y “O‘”. Dado un punto “A” del espacio tridimensional, podremos expresar sus coordenadas en ambos sistemas:
- OA = x ex + y ey + z ez.
- O’A = x’ ex’ + y’ ey’ + z’ ez.
Las coordenadas del origen “O” expresadas en sistema (x’, y’, z’) son:
- O’O = x0′ ex’ + y0′ ey’ + z0′ ez’.
A partir de las definiciones se cumple:
- O’A = O’O + OA = (x0′ ex’ + y0′ ey’ + z0′ ez’) + (x ex + y ey + z ez).
Expresemos ahora los vectores unitarios “ex“, “ey“, “ez“, en el sistema de vectores “ex’“, “ey’“, “ez’“:
- ex = a11 ex’ + a12 ey’ + a13 ez’.
- ey = a21 ex’ + a22 ey’ + a23 ez’.
- ez = a31 ex’ + a32 ey’ + a33 ez’.
Sustituyendo:
- O’A = (x0′ ex’ + y0′ ey’ + z0′ ez’) + (x a11 + y a21 + z a31) ex’ + (x a12 + y a22 + z a32) ey’ + (x a13 + y a23 + z a33) ez’, de donde: O’A = (x0′ + x a11 + y a21 + z a31) ex’ + (y0′ + x a12 + y a22 + z a32) ey’ + (z0′ + x a13 + y a23 + z a33) ez’.
De donde:
- x’ = x0′ + x a11 + y a21 + z a31.
- y’ = y0′ + x a12 + y a22 + z a32.
- z’ = z0′ + x a13 + y a23 + z a33.
En estas ecuaciones aparecen en los dos miembros coordenadas referidas al sistema nuevo. Esto permite una escritura más compacta, pero si queremos poner en cada miembro de las expresiones coordenadas referidas a un único sistema de referencia hemos de modificar:
- O’A = – OO + OA.
Siempre se cumple que:
- ex ex’ = a11.
- ey ex’ = a21.
- ez ex’ = a31.
- ex ey’ = a12.
- ey ey’ = a22.
- ez ey’ = a32.
- ex ez’ = a13.
- ey ez’ = a23.
- ez ez’ = a33.
Por lo tanto, si hacemos la descomposición inversa de los vectores:
- ex’ = a11 ex + a21 ey + a31 ez.
- ey’ = a12 ex + a22 ey + a32 ez.
- ez’ = a13 ex + a23 ey + a33 ez.
Para que la transformación lleve de un sistema de ejes ortogonales a otro ha de cumplirse:
- |ex|^2 = |ey|^2 = |ez|^2 = |ex’|^2 = |ey’|^2 = |ez’|^2 = 1.
- ex ey = ex ez = ey ez = ex’ ey’ = ex’ ez’ = ey’ ez’ = 0.
Todas estas ecuaciones conducen a:
- a11^2 + a12^2 + a13^2 = 1.
- a21^2 + a22^2 + a23^2 = 1.
- a31^2 + a32^2 + a33^2 = 1.
- a11 a21 + a12 a22 + a13 a23 = 0.
- a21 a31 + a22 a32 + a23 a33 = 0.
- a31 a11 + a32 a12 + a33 a13 = 0.
Es decir, la suma de los cuadrados de los elementos con alguna componente similar es “1”, y la suma de los productos dos a dos de las componentes de los vectores de la segunda base es “0”. A este tipo de transformaciones se les denomina ortogonales.
Un modo de obtener una transformación ortogonal usando parámetros con un claro significado geométrico es mediante los Ángulos de Euler. Sean dos sistemas coordenados (x, y, z) y (x’, y’, z’) que comparten el origen de coordenadas. Para determinar la posición de los ejes del sistema (x’, y’, z’) respecto a los ejes del sistema (x, y, z) basta con conocer los siguientes tres ángulos:
- El ángulo “σ” que forman los ejes zz’.
- El ángulo “Ψ” desde el eje “x'” a la recta “OH” de intersección del plano “xy” con el plano “x’y'”.
- El ángulo “φ” que forma la recta “OH” con el eje “x”.
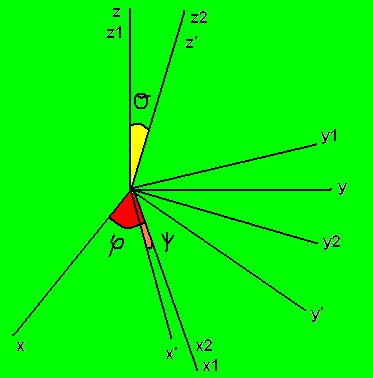
Al conjunto (φ, σ, Ψ) se le conoce como ángulos de Euler, y determinan completamente la posición de (x’, y’, z’) respecto a los ejes del sistema (x, y, z). El movimiento que lleva del triedro (x, y, z) al (x’, y’, z’) se puede descomponer en tres pasos:
.-Una rotación de un ángulo “φ” alrededor del eje “z”:
- x1 = x Cosφ + y Senφ.
- y1 = – x Senφ + y Cosφ.
- z1 = z.
.-Una rotación de un ángulo “σ” alrededor del eje “x” resultante (eje “OH”, que llamaremos eje “x2″):
- x2 = x1.
- y2 = y1 Cosσ + z1 Senσ.
- z2 = – y1 Senσ + z1 Cosσ.
.-Una rotación de un ángulo “ψ” alrededor del eje “z” resultante, que llamaremos eje “z3″:
- x’ = x2 CosΨ + y2 SenΨ.
- y’ = – x2 SenΨ + y2 CosΨ.
- z’ = z2.
En resumen:
- x’ = (Cosφ SenΨ – Senφ SenΨ Cosσ) x + (Senφ CosΨ + Cosφ SenΨ Cosσ) y + (SenΨ Senσ) z.
- y’ = – (Cosφ SenΨ – Senφ CosΨ Cosσ) x + (- Senφ SenΨ + Cosφ CosΨ Cosσ) y + (CosΨ Senσ) z.
- z’ = (Senφ Senσ) x – (Cosφ Senσ) y + (Cosσ) z.
Sistemas de Coordenadas Cilíndricas:
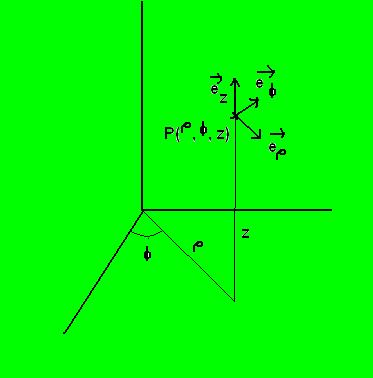
Consideremos un sistema de coordenadas cartesianas con ejes “x”, “y”, “z”. Las coordenadas cilíndricas de un punto serán denotadas por el radio “ρ”, la altura “z”, y el ángulo “Φ”; (ρ, Φ, z), y cumplen:
- x = ρ CosΦ.
- y = ρ SenΦ.
- z = z.
- ρ ≥ 0.
- 0 ≤ Φ ≤ 2 π.
- r = ρ CosΦ i + ρ SenΦ j + z k.
Las superficies de coordenadas constantes son:
- “ρ = cte” genera un cilindro de eje “z”.
- “Φ = cte” genera un plano que contiene al eje “z” y forma un ángulo “Φ” con el plano “xz”, siendo secante al plano “xy”.
- “z = cte” genera un plano horizontal de altura “z”.
Las transformaciones inversas son:
- ρ = [x^2 + y^2]^1/2.
- Φ = Arcotg(y / x).
- z = z.
Los vectores unitarios coordenados serán:
- ex = (dr / dx) / |dr / dx|, siendo “x” la coordenada curvilínea correspondiente.
A veces se definen los Coeficientes de Escala asociados a las coordenadas curvilíneas mediante hx = |dr / dx|. En nuestro caso:
- dr / dΦ = – ρ SenΦ i + ρ CosΦ j.
- dr / dρ = CosΦ i + SenΦ j.
- dr / dz = k.
- hΦ = ρ.
- hρ = 1.
- hz = 1.
Por lo tanto:
- eρ = CosΦ i + SenΦ j.
- eΦ = – SenΦ i + CosΦ j.
- ez = k.
Coordenadas Esféricas:
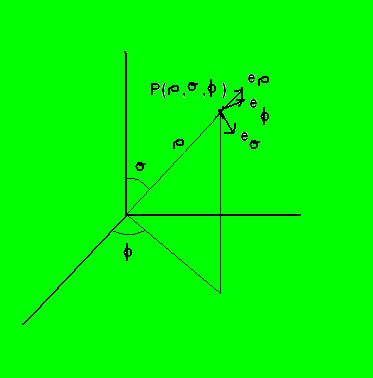
Denotaremos las coordenadas esféricas de un punto en el espacio por el radio “ρ”, el ángulo “σ” de latitud, y el ángulo “Φ” de corte con el plano ecuador, (ρ, σ, Φ), y verifican:
- x = ρ Senσ CosΦ.
- y = ρ Senσ SenΦ.
- z = ρ Cosσ.
- ρ ≥ 0.
- 0 ≤ Φ ≤ 2 π.
- 0 ≤ σ ≤ π.
- r = ρ Senσ CosΦ i + ρ Senσ SenΦ j + ρ Cosσ k.
Las relaciones recíprocas son:
- ρ = [x^2 + y^2 + z^2]^1/2.
- Φ = Arcotg(y / x).
- σ = Arcotg([x^2 + y^2]^1/2 / z).
Las superficies coordenadas correspondientes son:
- “ρ = cte” genera una esfera de centro “O”.
- “Φ = cte” genera un semiplano que contiene al eje “z” y forma un ángulo “Φ” con el eje “x”.
- “σ = cte” es un cono de semianchura “σ” y que posee al eje “z” como eje de simetría.
Además:
- dr / dρ = Senσ CosΦ i + Senσ SenΦ j + Cosσ k.
- dr / dσ = ρ Cosσ CosΦ i + ρ Cosσ SenΦ j – ρ Senσ k.
- dr / dΦ = – ρ Senσ SenΦ i + ρ Senσ CosΦ j.
- hρ = 1.
- hσ = ρ.
- hΦ = ρ Senσ.
Los vectores unitarios coordenados son entonces:
- er = Senσ CosΦ i + Senσ SenΦ j + Cosσ k.
- eσ = Cosσ CosΦ i + Cosσ SenΦ j – Senσ k.
- eΦ = – SenΦ i + CosΦ j.
El sistema de coordenadas esférico tiene sobre todo interés en la descripción de problemas con simetría esférica.
Ecuación de una Recta en el Espacio:
Dado un punto “P” de “R^3″ y un vector no nulo “u“, se llama recta que pasa por “P” y tiene por dirección “u” al conjunto de puntos que cumplen:
- Pi = P + λ u (ecuación vectorial).
En componentes obtenemos las ecuaciones paramétricas:
- pxi = px + λ ux.
- pyi = py + λ uy.
- pzi = pz + λ uz.
Dados dos puntos “P” y “Q” distintos, por ellos pasa una sola recta, cuyas ecuaciones paramétricas son:
- x = px + λ (qx – px).
- y = py + λ (qy – py).
- z = pz + λ (qz – pz).
Una recta que pase por un punto “P” con una dirección “u” coincide con otra que pase por “Q” con dirección “v” si los vectores “u“, “v“, “Q – P” son proporcionales. Si despejamos “λ” de las ecuaciones paramétricas obtendremos:
- λ = (x – px) / ux.
- λ = (y – py) / uy.
- λ = (z – pz) / uz.
, con lo que la recta queda también determinada por la llamada ecuación continua:
- (x – px) / ux = (y – py) / uy = (z – pz) / uz.
La recta que pasa por los puntos “P” y “Q” se puede escribir como:
- (x – px) / (qx – px) = (y – py) / (qy – py)= (z – pz) / (qz – pz).
Posición Relativa de Dos Rectas:
En el espacio dos rectas pueden ser paralelas, cortarse o cruzarse, de modo que la situación es algo más complicada que en el plano. Sean dos rectas que pasan por “P” y “Q” y tienen direcciones “u” y “v“, respectivamente. Sea “M” la matriz de coeficientes de determinante ecuación:
- |M| = (uy vz – vy uz) (qx – px) + (vx uz – ux vz) (qy – py) + (ux vy – vx uy) (qz – pz).
.- Si “u ≠ λ v“:
- Si “|M| ≠ 0″ las rectas de cruzan.
- Si “|M| = 0″ las rectas se cortan en un punto.
.- Si “u = λ v“:
- Si “Q – P ≠ λ u” las rectas son paralelas.
- Si “Q – P = λ u” las rectas son coincidentes.
Ecuación de un Plano:
En el espacio tridimensional un plano quedará determinado especificando un punto “P” por el que pase y la dirección dada por dos vectores “u” y “v” linealmente independientes. Un punto “X” pertenecerá al plano si existen dos coeficientes “λ”, “μ” tales que:
- Qi – P = λ ¬u + μ ¬v.
A ésta se le denomina ecuación vectorial del plano. Las ecuaciones paramétricas son:
- x = px + λ ux + μ vx.
- y = py + λ uy + μ vy.
- z = pz + λ uz + μ vz.
El plano que pasa por tres puntos no alineados P(px, py, pz), Q(qx, qy, qz), R(rx, ry, rz), lo podemos construir de la siguiente forma:
- x = px + λ (qx – px) + μ (rx – px).
- y = py + λ (qy – py) + μ (ry – py).
- z = pz + λ (qz – pz) + μ (rz – pz).
Ecuación Euclídea de un Plano:
Un plano del espacio “R^3″ queda determinado si se conoce uno de sus puntos “P” y un vector no nulo “n” ortogonal al plano. Un punto “Q” pertenecerá al plano si: (Q – P) n = 0, pues si este producto escalar es nulo serán perpendiculares. Ésta se conoce como la ecuación euclídea del plano.
La ecuación general de un plano en el espacio será:
- a x + b y + c z + d = 0.
, donde el vector n(a, b, c) es perpendicular al plano.
Rectas como Intersecciones de Planos:
Toda recta en el espacio tridimensional se puede expresar como intersección de dos planos cuyos vectores normales no son proporcionales. Así pues, podemos definir la recta “r” como:
- a1 x + b1 y + c1 z + d1 = 0.
- a2 x + b2 y + c2 z + d2 = 0.
, donde el vector normal al primer plano es m(a1, b1, c1) y el vector normal al segundo plano es n(a2, b2, c2).
Posicion Relativa de Rectas y Planos:
Sea un plano “π” de ecuación “a x + by + c z + d = 0″, y consideremos una recta “r” cuyo vector director es u(ux, uy, uz), y pasa por P(x0, y0, z0). Entonces la ecuación de la recta será: “(x – x0) / ux = (y – y0) / uy = (z – z0) / uz.”
El ángulo entre la recta y el plano “Φ” es el ángulo que forma el vector “u” con su proyección ortogonal sobre el plano “π”:
- Φ = Arcosen(u n / ||u|| ||a||).
Tenemos las siguientes posibilidades para la posición relativa de la recta y el plano:
- La recta y el plano se cortan en un punto si los vectores “u” y “n” no son perpendiculares.
- La recta y el plano son paralelos si los vectores “u” y “n” son perpendiculares y el sistema de ecuaciones es incompatible.
- La recta está contenida en el plano si los vectores “u” y “n” son perpendiculares y el sistema de ecuaciones es compatible.
Distancia de un Punto a un Plano:
Consideremos un punto “P” y un plano “π” tales que “P” no pertenezca a “π”. Entonces existe un punto “P0” en “π” tal que el vector “P – P0” es perpendicular a “π”. La distancia de “P” a “π” es la menor de las distancias de “P” a los puntos del plano “π”, y coincide con la longitud del segment0 PP0, que es la proyección del vector (Q – P) sobre la normal al plano, “n“, siendo “Q” un punto del plano:
- d(P,π) = |(Q – P) n| / ||n||.
Superficies y Curvas en el Espacio Tridimensional:
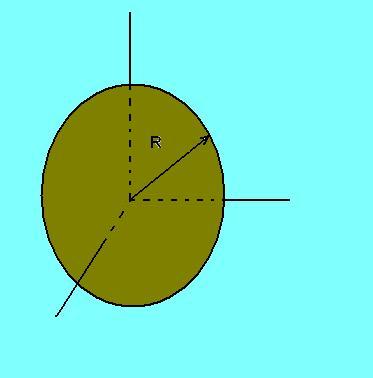
La ecuación de una superficie en el espacio tridimensional puede escribirse como f(x, y, z) = 0, y se denomina ecuación implícita de la superficie. Los puntos cuyas coordenadas (x, y, z) satisfacen dicha ecuación forman parte de la superficie. Un ejemplo es la esfera de radio “R” con centro en (x0, y0, z0):
- (x – x0)^2 + (y – y0)^2 + (z – zo)^2 = R^2.
Otra forma de escribir la ecuación de una superficie es mediante el uso de parámetros. En general, si “u”, “v” pertenecen a “R”, una superficie podrá escribirse como:
- x = f1(u, v).
- y = f2(u, v).
- z = f3(u, v).
Éstas se conocen como las componentes paramétricas de la superficie.
Veamos por ejemplo las de la esfera (coordenadas esféricas):
- x = R Senσ CosΦ.
- y = R Senσ SenΦ.
- z = R Cosσ.
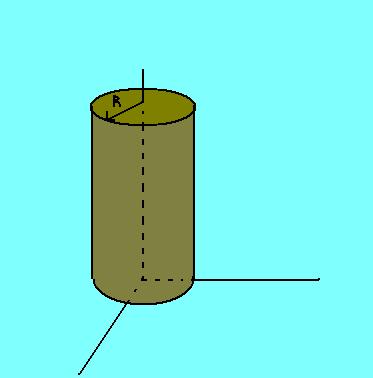
Otro ejemplo. Consideremos el cilindro de radio “R” y que tiene como eje el eje “z”. Los puntos que se encuentran sobre el cilindro verifican que su distancia al eje debe ser “R”, de modo que tenemos la ecuación:
- x^2 + y^2 = R^2, para cualquier valor de “z”.
Sus ecuaciones paramétricas podrían ser (coordenadas cilíndricas):
- x = R CosΦ.
- y = R SenΦ.
- z = z.
Si intersecamos dos superficies tendremos en general una curva, de modo que al conjunto de de ecuaciones:
- f1(x, y, z) = 0.
- f2(x, y, z) = 0.
se les denomina a veces ecuación de una curva en forma implícita.
Consideremos las ecuaciones:
- x^2 + y^2 = R^2.
- x = h.
Se trata de un cilindro de radio “R” y un plano paralelo al plano “xy” que pasa por “x = h”. Tomadas en conjunto, esas dos ecuaciones describen una circunferencia de radio “R” centrada en (0, 0, h).
Otra forma de escribir la ecuación de una curva en 3 dimensiones es mediante un cierto parámetro, con lo cual tenemos las ecuaciones paramétricas de la curva:
- x = g1(t).
- y = g2(t).
- z = g3(t).
En el caso de la circunferencia anterior tendríamos:
- x = R Cost.
- y = R Sent.
- z = h.
Finalmente, una curva y una superficie intersecan normalmente en uno o varios puntos.
Superficies de Revolución:
Supongamos una curva en el plano “xz” dada mediante la ecuación z = f(x). Si giramos esta curva alrededor del eje “z”, cada punto de la curva describirá una circunferencia con centro en el punto (0, 0, z0), y radio “x0″. Los puntos de esta circunferencia verifican entonces:
- x^2 + y^2 = x0^2.
- z = z0.
Tenemos entonces “z0 = f([x^2 + y^2]^1/2). La ecuación de la superficie de revolución generada podemos escribirla como:
- z = f([x^2 + y^2]^1/2) = f(r).
Superficies Cilíndricas:
Sea “γ” cierta curva en el espacio y sea “¬u” una dirección. Denominaremos superficie cilíndrica de curva directriz “γ” y de generatriz “¬u” a la superficie contruida haciendo pasar por cada punto de “γ” una recta paralela a “¬u”.
Consideremos por ejemplo la siguiente elipse en el plano “xy”:
- x0^2 / a^2 + y0^2 / b^2 = 1.
Si tomamos la generatriz paralela al eje “z” (ux = uy = 0, uz = 1), tendremos la ecuación de un cilindro elínptico de generatriz “z”:
- x^2 / a^2 + y^2 / b^2 = 1.
Si tomamos, sin embargo, la recta “x = z, y = 0″ por generatriz, obtendremos un cilindro elíptico de generatriz “x = z, y = 0″ (ux = uy = 0, uz = 1):
- (x – z)^2 / a^2 + y^2 / b^2 = 1.
Superficies Cónicas:
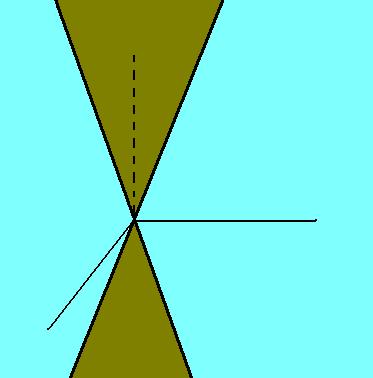
Sea “γ” una curva arbitraria y “O” un punto fuera de ella. Tracemos una recta por cada punto de “γ” que pasa por “O”. El conjunto de puntos situados en estas rectas se denomina superficie cónica. “γ” es la directriz, “O” es el vértice, y cada recta “l” que pase por “γ” y “O” se denomina generatriz.
Supongamos que el vértice está situado en el origen de coordenadas, y tomemos como generatriz una recta que pase por “O” y por un punto (x0, y0, z0) de la curva “γ”. Las ecuaciones paramétricas de esta generatriz serán:
- x = t x0.
- y = t y0.
- z = t z0.
Y su ecuación implícita es:
- f1(x0, y0, z0) = 0.
- f2(x0, y0, z0) = 0.
Como (x0, y0, z0) pertenece a la curva, y por lo tanto definible en general por medio a dunas ecuaciones paramétricas, ha de verificarse que:
- x0 = g1(u).
- y0 = g2(u).
- z0 = g3(u).
de donde:
- x = t g1(u).
- y = t g2(u).
- z = t g3(u).
Éstas serían las ecuaciones paramétricas de una superficie cónica con el vértice en el origen de coordenadas. Su ecuación implícita vendría dada por:
- F(x, y, z) =0.
, por lo tanto podemos escribir:
- F(x, y, z) = F(t x0, t y0, t z0) = F(x0, y0, z0) = 0.
Una propiedad interesante que se deriva de esto es que cualquier función homogénea de grado “q”:
- F(t x, t y, t z) = t^q F(x, y, z).
puede representar una superficie cónica con vértice en el origen si la escribimos como:
- F(x, y, z) = 0.
En efecto, si el punto (x0, y0, z0) está en la superficie tenemos:
- F(x0, y0, z0) = F(t x0, t y0, t z0) = t^q F(x0, y0, z0).
Por lo tanto los puntos de las rectas que pasan por el origen está en la superficie.
El Elipsoide:
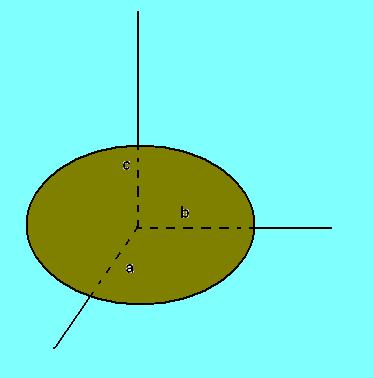
Consideremos en el espacio euclídeo un sistema de ejes rectangulares “xyz”, y sean los números reales:
- a > 0.
- b > 0.
- c > 0.
Definimos los puntos:
- A = (a, 0, 0).
- A’ = (- a, 0, 0).
- B = (0, b, 0).
- B’ = (0, – b, 0).
- C = (0, 0, c).
- C’ = (0, 0, – c).
Sean las elipses siguientes:
- “Ex” con ejes “BB'”, “CC'”.
- “Ey” con ejes “AA'”, “CC'”.
- “Ez” con ejes “AA'”, “BB'”.
Cuyas ecuaciones son:
.-Ex:
- y^2 / b^2 + z^2 / c^2 = 1.
- x = 0.
.-Ey:
- x^2 / a^2 + z^2 / c^2 = 1.
- y = 0.
.-Ez:
- x^2 / a^2 + y^2 / b^2 = 1.
- z = 0.
Se llama elipsoide de vértices “A”, “A'”, “B”, “B'”, “C”, “C'”, al lugar geométrico que describe una elipse situada en un plano perpendicular al eje “z”, y que tiene sus vértices en las elipses “Ex”, “Ey”. La ecuación reducida del elipsoide es:
- x^2 / a^2 + y^2 / b^2 + z^2 / c^2 = 1.
Un plano perpendicular al eje “z”, tal como el:
- z = h.
, corta a la elipse “Ex” en los puntos:
- y^2 / b^2 + h^2 / c^2 = 1.
- x = 0.
, y a la elipse “Ey” en los puntos:
- x^2 / a^2 + h^2 / c^2 = 1.
- y = 0.
Es decir, por un lado a los puntos:
- y = +- b [1 – h^2 / c^2]^1/2.
- x = 0.
- z = h.
, y por el otro a los puntos:
- x = +- a [1 – h^2 / c^2]^1/2.
- y = 0.
- z = h.
De aquí deducimos que uno de los semiejes de la elipse variable por longitud “a [1 – h^2 / c^2]^1/2″ (el correspondiente al eje “x”), y el otro tiene por longitud “b [1 – h^2 / c^2]^1/2″ (el correspondiente al eje “y”).
La ecuación de la elipse resultado de la intersección del elipsoide con un plano:
- z = h.
es, por lo tanto:
- z = h.
- x^2 / (a^2 (1 – h^2 / c^2)) + y^2 / (b^2 (1 – h^2 / c^2)) = 1.
- – c ≤ h ≤ c.
El lugar geométrico que barre esta elipse variando “h” desde “- c” hasta “c” es la superficie del elipsoide.
Propiedades del Elipsoide:
El elipsoide:
- x^2 / a^2 + y^2 / B`2 + z^2 / c^2 = 1.
es simétrico respecto al origen de coordenadas. También es simétrico respecto a los ejes “x”, “y”, “z”, y respecto a los planos coordenados:
- x = 0.
- y = 0.
- z = 0.
El elipsoide está situado entre dos esferas cuyos radios son:
- r = mínimo de (a, b, c).
- R = máximo de (a, b, c).
Si:
- a = b.
, entonces el elipsoide es de revolución alrededor del eje “z”. Si además:
- a = b = c.
, se trata de una esfera de radio “a”. Si:
- a = c.
, tenemos una elipsoide de revolución alrededor del eje “y”.
Hiperboloide de una hoja:
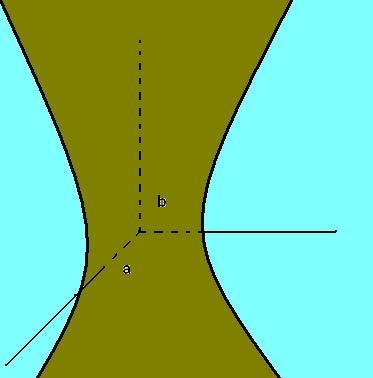
Consideremos un sistema de ejes rectangulares “xyz”, y sean los números reales:
- a > 0.
- b > 0.
- c > 0.
Definimos los puntos:
- A = (a, 0, 0).
- A’ = (- a, 0, 0).
- B = (0, b, 0).
- B’ = (0, – b, 0).
- C = (0, 0, c).
- C’ = (0, 0, – c).
- Sea “E” la elipse de simejes “AA'” y “BB'”.
- Sea “Hx” la hipérbola con el eje real “BB'” e imaginario “CC'”.
- Sea “Hy” la hipérbola con eje real “AA'” e imaginario “CC'”.
El hiperboloide de una hoja con ejes reales “AA'”, “BB'”, y cuyo eje imaginario es “CC'”, es el lugar geométrico de los puntos que pertenecen a una elipse situada en un plano perpendicular a “z” y con vértices en las hipérbolas “Hx” y “Hy”. Su ecuación reducida es:
- x^2 / a^2 + y^2 / b^2 – z^2 / c^2 = 1.
Las ecuaciones de la elipse “E” son:
- x^2 / a^2 + y^2 / b^2 = 1.
- z = 0.
Las de la hipérbola “Hx”:
- y^2 / b^2 – z^2 / c^2 = 1.
- x = 0.
Y las de la hipérbola “Hy”:
- x^2 / a^2 – z^2 / c^2 = 1.
- y = 0.
Si cortamos estas hipérbolas “Hx” y “Hy” con el plano horizontal:
- z = h.
obtendremos los siguientes puntos de corte: por parte de “Hx:”
- y = +- b [1 + h^2 / c^2]^1/2.
- x = 0.
- z = h.
y por parte de “Hy”:
- x = +- a [1 + h^2 / c^2]^1/2.
- y = 0.
- z = h.
Por lo tanto la elipse resultado de la intersección del hiperboloide con el plano:
- z = h.
será:
- z = h.
- x^2 / (a^2 (1 + h^2 / c^2)) + y^2 / (b^2 (1 + h^2 / c^2)) = 1.
- – ∞ ≤ h ≤ ∞.
Al hacer variar esta elipse en el eje “z” obtenemos la superficie del hiperboloide de una hoja. Si eliminamos “h” de las dos ecuaciones anteriores obtendremos la ecuación reducida.
Propiedades del Hiperboloide de Una Hoja:
El hiperboloide:
- x^2 / a^2 + y^2 / b^2 – z^2 / c^2 = 1.
es simétrico respecto al origen “O”, a los ejes “x”, “y” y “z”, y también respecto a los planos coordenados.
El hiperboloide está situado fuera del cono:
- x^2 / a^2 + y^2 / b^2 – z^2 / c^2 = 0.
Este cono es asintótico al hiperboloide, y es el cono que generan las asíntotas que resultan de cortar al hiperboloide con planos que contienen al eje “z”.
Sabemos que la intersección del hiperboloide con el plano:
- z = h.
es:
- x^2 / (a^2 (1 + h^2 / c^2)) + y^2 / (b^2 (1 + h^2 / c^2)) = 1.
, mientras que la intersección del cono con ese mismo plano es:
- x0^2 / (a^2 h^2 / c^2) + y0^2 / (b^2 h^2 / c^2) = 1.
Si un punto (x0, y0) cumple la anterior ecuación, entonces el punto:
- x = [1 + h^2 / c^2]^1/2 x0 / (h / c).
- y = [1 + h^2 / c^2]^1/2 y0 / (h / c).
cumple pertenecer a la intersección con el hiperboloide. Los puntos (x, y) y (x0, y0) están en un plano perpendicular al eje “z”, y sus distancias a este eje verifican:
- d = [x^2 + y^2]^1/2 = [c^2 / h^2 + 1]^1/2 [x0^2 + y0^2]^1/2.
- d ≥ d0 = [x0^2 + y0^2]^1/2.
La ecuación del hiperboloide en coordenadas cilíndricas es:
- ρ^2 (CosΦ^2 / a^2 + SenΦ^2 / b^2) – z^2 / c^2 = 1.
La intersección de este hiperboloide con un plano:
- Φ = cte.
es una hipérbola. Las asíntotas de esta hipérbola son las rectas que admiten por ecuación conjunta a:
- ρ^2 (CosΦ^2 / a^2 + SenΦ^2 / b^2) = z^2 / c^2.
El lugar geométrico que engendran estas rectas es el cono antes descrito.
Si:
- a = b.
, entonces el hiperboloide de revolución gira en torno al eje “z”.
Hiperboloide de dos hojas:
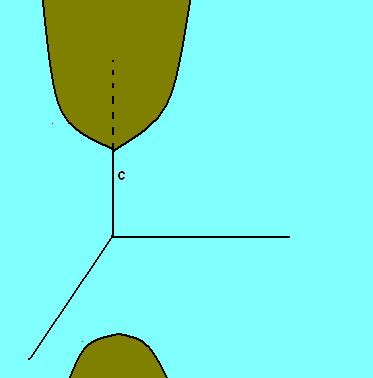
Consideremos un sistema de ejes rectangulares “xyz”, y sean los números reales:
- a > 0.
- b > 0.
- c > 0.
Definimos los puntos:
- A = (a, 0, 0).
- A’ = (- a, 0, 0).
- B = (b, 0, 0).
- B’ = (- b, 0, 0).
- C = (c, 0, 0).
- C’ = (- c, 0, 0).
- Sea “Hx” la hipérbola con eje real “CC'” e imaginario “BB'”.
- Sea “Hy” la hiperbola con eje real “CC'” e imaginario “AA'”.
Se llama hiperboloide de dos hojas, que tiene como eje real “CC'” y como ejes imaginarios “AA'” y “BB'”, al lugar geométrico que describe una elipse variable situada en un plano perpendicular al eje “z” y cuyos vértices están en las hipérbolas “Hx” y “Hy”. Su ecuación reducida es:
- x^2 / a^2 + y^2 / b^2 – z^2 / c^2 = – 1.
La hipérbola “Hx” es:
- y^2 / b^2 – z^2 / c^2 = 1.
- x = 0.
Y la hipérbola “Hy” es:
- x^2 / a^2 – z^2 / c^2 = 1.
- y = 0.
Si cortamos al hiperboloide con un plano:
- z = h.
obtenemos dos elipses con vértices en los puntos:
- y^2 / b^2 – z^2 / c^2 = 1.
- x = 0.
- z = h.
y:
- x^2 / a^2 – z^2 / c^2 = 1.
- y = 0.
- z = h.
La ecuación de la elipse será:
- x^2 / (a^2 (h^2 / c^2 – 1)) + y^2 / (b^2 (h^2 / c^2 – 1)) = 1.
- |h| ≥ c.
Propiedades del Hiperboloides de Dos Hojas:
El hiperboloide de dos hojas es simétrico respecto al origen “O”, respecto a los ejes “x”, “y”, “z”, y también respecto a los planos coordenados.
El hiperboloide se halla situado fuera de la región:
- |z| < c.
, ya que:
- z^2 / c^2 = 1 + x^2 / a^2 + y^2 / b^2 ≥ 1.
Si:
- a = b.
, entonces el hiperboloide es de revolucion:
- (x^2 + y^2) / a^2 – z^2 / c^2 = 1.
, resultado de hacer girar alrededor del eje “z” una hipérbola conjugada al caso del hiperboloide de una hoja.
Paraboloide Elíptico:
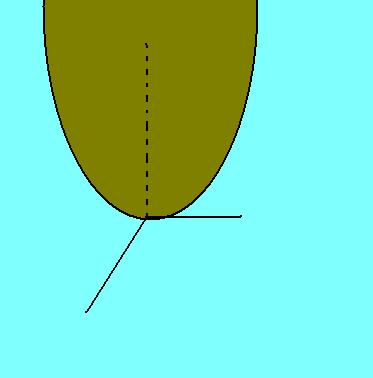
Consideremos en un sistema de semiejes rectangulares las siguientes parábolas: “Py”:
- x^2 = 2 p z.
- y = 0.
“Px”:
- y^2 = 2 q z.
- x = 0.
- p > 0.
- q > 0.
Tienen el vértice en el origen, la concavidad en el mismo sentido, y están situadas en planos perpendiculares.
El paraboloide elíptico es el lugar geométrico que describe una elipse variable con vértices en “Px” y “Py”. Su ecuación reducida es:
- x^2 / p + y^2 / q = 2 z.
Si cortamos este paraboloide con un plano:
- z = h.
obtenemos los siguientes puntos de corte por parte de “Px”:
- x = +- [2 p h]^1/2.
- y = 0.
- z = h.
, y por parte de “Py”:
- y = +- [2 q h]^1/2.
- x = 0.
- z = h.
La elipse resultado de la intersección será:
- x^2 / 2 p h + y^2 / 2 q h = 1.
Propiedades del Paraboloide Elíptico:
El punto “O” se llama vértice de paraboloide elíptico, pero no es un centro de simetría. El paraboloide es simétrico respecto al eje “z” y los planos:
- x = 0.
- y = 0.
Si cortamos el paraboloide con los planos:
- x = cte.
ó:
- y = cte.
, obtenemos las parábolas:
- x = c.
- c^2 / 2 p + y^2 / 2 q = z.
- y^2 = 2 q z – q c^2 / p.
, y:
- y = c.
- x^2 / 2 p + c^2 / 2 q = z.
- x^2 = 2 p z – p c^2 / q.
Si:
- p = q.
, entonces el paraboloide es de revolución, resultado de girar una parábola con el centro en el origen alrededor del eje “z”:
- x^2 + y^2 = 2 p z.
Paraboloide Hiperbólico:

Consideremos un sistema de ejes coordenados rectangulares y a las siguientes parábolas: Px:
- y^2 = – 2 q z.
- x = o.
Py:
- x^2 = 2 p z.
- y = 0.
- p > 0.
- q > 0.
Tienen el mismo vértice, la concavidad en distinto sentido, y están situadas en planos perpendiculares. Se llama paraboloide hiperbólico al lugar geométrico que describe una parábola variable paralela a “Px” que se desplaza de manera que su vértice recorre “Py”. Su ecuación reducida es:
- x^2 / p – y^2 / q = 2 z.
Si intersecamos el paraboloide con:
- y = h.
obtenemos:
- x^2 / p = 2 z + h^2 / q.
- x^2 = 2 p (z + h^2 / 2 q).
, que es una parábola en el plano:
- y = h.
, con vértice (0, h, – h^2 / 2 q). Análogamente, si intersecamos el paraboloide con el plano:
- x = h.
, obtenemos:
- – x^2 / p = 2 z – h^2 / q.
- x^2 = – 2 p (z – h^2 / 2 q).
, que es una parábola en el plano:
- x = h.
con vértice (h, 0, h^2 / 2 q).
Si intersecamos al paraboloide hiperbólico con planos:
- z = h.
obtenemos hipérbolas conjugadas:
- x^2 / p – y^2 / q = 2 h.
- x^2 / 2 h p – y^2 / 2 h q = 1, si h > 0.
- x^2 / |2 h p| – y^2 / |2 h q| = 1, si h < 0.
Al paraboloide hiperbólico se le llama a veces “superficie en silla de montar”, por su analogía con ella.
Propiedades del Paraboloide Hiperbólico:
Se denomina vértice del paraboloide hiperbólico al punto “O”. Es simétrico respecto a “z” y a los planos:
- x = 0.
- y = 0.
Esta superficie no es en ningún caso una superficie de revolución.