La historia de la fórmula de Baker-Campbell-Hausdorff (BCH) se inició en 1890 e involucra a Schur, Campbell, Poincaré, Baker, Pascal, Hausdorff, Yoshida y Dynkin. Para números reales se tiene que z=log(exp(x) exp(y))= x+y. Sin embargo, para matrices Z=log(exp(X) exp(Y)) ≠ X+Y, salvo cuando éstas conmutan [X,Y]=XY–YX =0. La fórmula BCH tiene infinitos términos, aunque en muchas aplicaciones se trunca por un número finito de ellos.
Supongo que si has estudiado mecánica cuántica sabrás que para [X,Y]= c I, se cumple que Z=X+Y+[X,Y]/2; esta expresión se aplica al conmutador de Heisenberg [P,Q]=–i ℏ I. Me ha resultado muy curioso que cuando [X,Y] = u X + vY + c I, se cumple que Z=X+Y+f(u,v)[X,Y].
Por supuesto, en estas expresiones u, v y c son números (reales o complejos). La demostración en Alexander Van-Brunt, Matt Visser, “Special-case closed form of the Baker-Campbell-Hausdorff formula,” arXiv:1501.02506 [math-ph], 11 Jan 2015.
Por cierto, la fórmula BCH fue usada por primera vez por el matemático germano Friedrich Schur (1856–1932) en 1890, por el irlandés John Edward Campbell (1862–1924) en 1897, por el francés Jules Henri Poincaré (1854–1912) en 1899, por el británico Henry Frederick Baker (1866–1956) en 1901, por el italiano Ernesto Pascal (1865–1940) en 1901, por el germano Felix Hausdorff (1868–1942) en 1906, por el japonés KōsakuYoshida (1909–1990) en 1937, y por el soviético Eugene Borisovich Dynkin (1924–2014) en 1947. Todos ellos afirmaron haber descubierto la fórmula sin conocimiento del trabajo de los otros. Por ello, en rigor, se debería llamar fórmula de Schur–Campbell–Poincaré–Baker–Pascal–Hausdorff–Yoshida–Dynkin.
Nos cuentan esta apasionante historia Rüdiger Achilles y Andrea Bonfiglioli, “The early proofs of the theorem of Campbell, Baker, Hausdorff, and Dynkin,” Arch. Hist. Exact Sci. 66: 295-358, 2012.
No quiero entrar en detalles de la demostración de Van-Brunt–Visser. Para ![[X,Y]=u\,X+v\,Y+c\,I](http://s.wordpress.com/latex.php?latex=%5BX%2CY%5D%3Du%5C%2CX%2Bv%5C%2CY%2Bc%5C%2CI&bg=T&fg=111111&s=0 "[X,Y]=u\,X+v\,Y+c\,I")
obtienen que
obtienen que![Z(X,Y)=\log(e^X\,e^Y)=X+Y+f(u,v)\,[X,Y],](http://s.wordpress.com/latex.php?latex=Z%28X%2CY%29%3D%5Clog%28e%5EX%5C%2Ce%5EY%29%3DX%2BY%2Bf%28u%2Cv%29%5C%2C%5BX%2CY%5D%2C&bg=T&fg=111111&s=0 "Z(X,Y)=\log(e^X\,e^Y)=X+Y+f(u,v)\,[X,Y],")
donde la función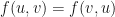 
está dada por
está dada por
La aplicación de esta fórmula a los operadores de creación y aniquilación de partículas en el formalismo de segunda cuantización es realmente interesante. Como tenemos ![[a,a^\dagger]=I,](http://s.wordpress.com/latex.php?latex=%5Ba%2Ca%5E%5Cdagger%5D%3DI%2C&bg=T&fg=111111&s=0 "[a,a^\dagger]=I,")
se obtienen expresiones tan curiosas como
se obtienen expresiones tan curiosas como![[a^2,(a^\dagger)^2]=4\,(a^\dagger\,a)+2\,I=4\,N+2\,I,](http://s.wordpress.com/latex.php?latex=%5Ba%5E2%2C%28a%5E%5Cdagger%29%5E2%5D%3D4%5C%2C%28a%5E%5Cdagger%5C%2Ca%29%2B2%5C%2CI%3D4%5C%2CN%2B2%5C%2CI%2C&bg=T&fg=111111&s=0 "[a^2,(a^\dagger)^2]=4\,(a^\dagger\,a)+2\,I=4\,N+2\,I,")
![[a^2,(a^\dagger\,a)]=[a^2,N]=2\,a^2,](http://s.wordpress.com/latex.php?latex=%5Ba%5E2%2C%28a%5E%5Cdagger%5C%2Ca%29%5D%3D%5Ba%5E2%2CN%5D%3D2%5C%2Ca%5E2%2C&bg=T&fg=111111&s=0 "[a^2,(a^\dagger\,a)]=[a^2,N]=2\,a^2,")
![[(a^\dagger)^2,(a^\dagger\,a)]=[(a^\dagger)^2,N]=-2\,(a^\dagger)^2.](http://s.wordpress.com/latex.php?latex=%5B%28a%5E%5Cdagger%29%5E2%2C%28a%5E%5Cdagger%5C%2Ca%29%5D%3D%5B%28a%5E%5Cdagger%29%5E2%2CN%5D%3D-2%5C%2C%28a%5E%5Cdagger%29%5E2.&bg=T&fg=111111&s=0 "[(a^\dagger)^2,(a^\dagger\,a)]=[(a^\dagger)^2,N]=-2\,(a^\dagger)^2.")
Y muchas más. La verdad, creo que merece la pena recordar la fórmula de Van-Brunt–Visser.
