alquimiayciencias: Mecánica cuántica from a dummy. (Que no te lo cuenten /3 )

Hay un extraño sentimiento de felicidad cuando uno es capaz de realizar algún cálculo que se presupone difícil.

En las últimas dos entradas sobre el tema que estamos tratando hemos ido introduciendo un poco del formalismo matemático de la cuántica.

Sin duda alguna, el nivel es muy superficial pero aún así nos permite disfrutar un poco de lo que es “hacer” cuántica de verdad.

Valores esperados del color

Tenemos un operador color que denotamos por: $\hat{C}$ .

Este operador tiene dos estados propios, estado blanco y estado negro.

Son propios porque al actuar el operador sobre ellos los deja iguales y multiplicados por un número:

Para simplificar vamos a reescribir esas relaciones por:

$\hat{C}|b\rangle=+1|b\rangle$

$\hat{C}|n\rangle=-1|n\rangle$

donde $|b\rangle, |n\rangle$ representan, respectivamente los estados blanco y negro.

Ahora vamos a calcular el valor esperado del operador color sobre el estado blanco:

$\langle\hat{C}\rangle_{|b\rangle}=\langle b|\hat{C}|b\rangle$

Paso 1:

Los operadores siempre actúan sobre el objeto que tengan a su derecha. Como sabemos que 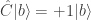$\hat{C}|b\rangle=+1|b\rangle$ obtenemos:

$\langle b|\hat{C}|b\rangle=\langle b|(+1)|b\rangle$

Paso 2:

Los números reales, como el +1, salen de ese paréntesis como si nada, con lo que nos queda:

$\langle b|(+1)|b\rangle=(+1)\langle b|b\rangle$

Paso 3:

Sabemos lo que vale el producto de un estado propio por sí mismo, $\langle b|b\rangle=1$ . Por lo tanto:

$\langle \hat{C}\rangle_{|b\rangle}=(+1)\langle b|b\rangle=(+1)1=+1$

Ese es el resultado del valor esperado del operador color para el estado blanco.

Si queremos calcular el valor esperado del operador color para el estado negro solo tenemos que seguir los pasos con cuidado:

$\langle \hat{C}\rangle_{|n\rangle}=\langle n|\hat{C}|n\rangle$

$\langle n|\hat{C}|n\rangle=\langle n|(-1)|n\rangle$

$\langle n|(-1)|n\rangle=(-1)\langle n|n\rangle=(-1)1$

Queda por lo tanto:

$\langle \hat{C}\rangle_{|n\rangle}=-1$

Ese es el valor esperado del operador C sobre su estado propio negro.

Que pasa si tenemos un estado que es superposición de blanco y negro, es decir, que sea una suma y restad de los estados blanco y negros multiplicados por unos determinados coeficientes:

$|\psi\rangle=a|b\rangle+b|n\rangle$

El valor esperado del operador C sobre este estado será:

$\langle \hat{C}\rangle_{|\psi\rangle}=\langle \psi|\hat{C}|\psi\rangle$

$\langle \psi|\hat{C}|\psi\rangle=(a\langle b|+b\langle n|)\hat{C}(a|b\rangle+b|n\rangle)$

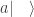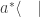En este punto vamos a asumir por simplicidad que a y b son coeficientes numéricos reales (con complejos lo único que cambia es que al pasar de $a|\phantom{ab}\rangle$ a $a^*\langle \phantom{ab}|$ hay que pasar el número a su complejo conjugado).

Ahora hacemos todas las posibles agrupaciones usando la ley distributiva.

$(a\langle b|+b\langle n|)\hat{C}(a|b\rangle+b|n\rangle)=$

$=a^2\langle b|\hat{C}|b\rangle +$

$+ab\langle b|\hat{C}|n\rangle+$

$+ ba\langle n |\hat{C}| b\rangle+$

$+b^2 \langle n|\hat{C}|n\rangle=$

Procedemos como antes, viendo cual es la actuación del operador sobre el estado de su derecha, ese es el orden de acción natural de los operadores:

$(a\langle b|+b\langle n|)\hat{C}(a|b\rangle+b|n\rangle)=$

$=a^2\langle b|(+1)|b\rangle +$

$+ab\langle b|(-1)|n\rangle+$

$+ ba\langle n |(+1)| b\rangle+$

$+b^2 \langle n|(-1)|n\rangle=$

Sacamos los números fuera de esos paréntesis raros:

$(a\langle b|+b\langle n|)\hat{C}(a|b\rangle+b|n\rangle)=$

$=(+1)a^2\langle b|b\rangle +$

$+(-1)ab\langle b|n\rangle+$

$+ (+1)ba\langle n | b\rangle+$

$+(-1)b^2 \langle n|n\rangle=$

Recordando los productos entre estados propios dados por:

Las expresiones anteriores quedan:

$(a\langle b|+b\langle n|)\hat{C}(a|b\rangle+b|n\rangle)=$

$=(+1)a^2\times (1)+$

$+(-1)ab\times (0)+$

$+ (+1)ba\times (0)+$

$+(-1)b^2 \times (1)=$

Con lo que la cosa queda:

$(a\langle b|+b\langle n|)\hat{C}(a|b\rangle+b|n\rangle)=$

$(+1)a^2\times (1)+$

$+(-1)b^2 \times (1)=$

Por lo tanto, el valor esperado del operador C en el estado superpuesto $|\psi\rangle$ es:

$\langle \hat{C}\rangle_{|\psi\rangle}=a^2-b^2$

No tiene ningún misterio :)

¿Para qué vale todo esto?

Imaginemos que tenemos un aparato de medir el color tal que este:

¿Qué nos responderá el aparato si introducimos un sistema cuántico en el estado blanco? Supongo que la respuesta es fácil de responder:

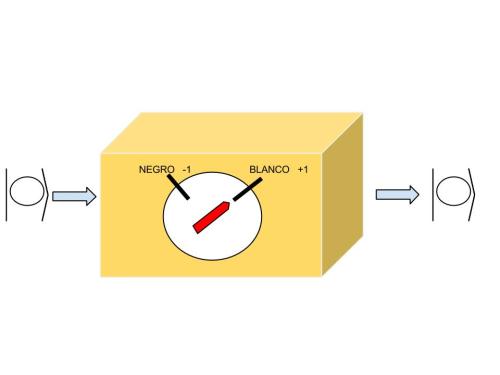
Eso es porque el estado blanco es estado propio del operador color $\hat{C}$ .

Ese operador representa en cierto modo la característica que queremos medir. La cuántica nos dice que al medir sobre el estado propio obtendremos como resultado de la medida el valor del coeficiente que multiplica al estado después de hacer actuar su operador sobre él.

Otro aspecto importante es que el estado permanece inalterado en la medida, sale exactamente igual que entró. Eso implica que si encadenamos un conjunto de medidas sobre el color estaríamos en este caso:

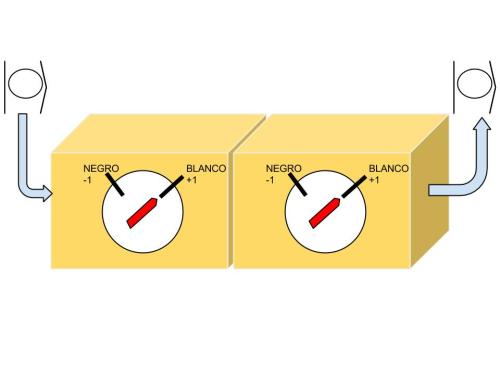
Un caso análogo lo tendríamos con el estado propio negro.

¿Qué ocurre si intentamos medir sobre un estado superpuesto?

Pues que nos dará blanco o negro pero no sabemos predecir cual de ellos obtendremos en una única media.

Que salga blanco o negro es totalmente aleatorio.

Recordemos que el estado superpuesto tenía la forma:

Bien, intentemos predecir el resultado de la medida. Tal vez la aguja del aparato de medida se quede en un punto intermedio entre el blanco y el negro, indicando la superposición.

Suponemos que si el coeficiente del estado blanco es mayor que el coeficiente del estado negro la aguja estará entre ambos resultados, blanco y negro, pero un poco más cerca del blanco que del negro.

Esa es la intuición inicial, al menos la mía.

Pero esa es una lectura incorrecta de los estados cuánticos.

La razón principal es que en cuántica los únicos resultados posibles para la medida de un estado superpuesto, son los valores asociados a los estados propios que forman parte de la superposición.

Es decir, el resultado de cualquier medida de color nos dará blanco o negro, +1 o -1, pero nada intermedio.

Por lo tanto, ¿Si introducimos el estado $|?\rangle$ en el aparato de medida qué obtendremos?

La respuesta es:

O bien:

No tenemos ni idea de lo que vamos a obtener en un única medida. Entonces de qué sirve la cuántica si a final de cuentas no podemos predecir el resultado de medida alguna. Un fiasco total de teoría por lo que parece.

Bueno, la cosa no es tan dramática.

Resulta que si repetimos las medidas sobre un número ingente de estados idénticos $|?\rangle$ , en cada medida no podemos predecir el resultado obteniendo pero…

Resulta que la proporción en la que no sale blanco es 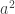$a^2$ por cien y en la que sale negro es $b^2$ por cien.

Por eso es por lo que se exige que

$a^2+b^2=1$

Porque estos coeficientes de la superposición nos indican la probabilidad con la que aparecen los valores permitidos de las medidas.

Así que lo que hacemos es calcular el valor esperado del operador con un estado dado, por ejemplo:

$|?\rangle=\frac{1}{\sqrt{2}}|b\rangle+\frac{1}{\sqrt{2}}|n\rangle$

o en este:

$|?\rangle=\frac{1}{\sqrt{4}}|b\rangle+\frac{\sqrt{3}}{\sqrt{4}}|n\rangle$

¿Cuánto vale el valor esperado del operador de color en estos estados?

Experimentalmente lo que se hace es repetir las medidas muchas veces y ver como se recupera el valor esperado teórico calculado sobre el estado con el que estemos trabajando.

La cuántica es maravillosa.

Nos seguimos leyendo…

alquimiayciencias

miércoles, 23 de septiembre de 2015

Mecánica cuántica from a dummy. (Que no te lo cuenten /3 )

Valores esperados del color

¿Para qué vale todo esto?

Datos personales

Archivo del blog