alquimiayciencias: En un universo hecho de materia…

El primer caso que vamos a tratar es: Un universo con únicamente materia no relativista.

El contenido del universo

Recordemos que el contenido del universo se identifica por las ecuaciones de estado, es decir, las relaciones entre la presión que produce el contenido con su densidad. En el caso de materia (no relativista) la ecuación de estado es muy simple P=0.

Resolvamos la ecuación de la densidad

$\dot{\rho}+3\dfrac{\dot{a}}{a}\left(\rho+\dfrac{P}{c^2}\right)=0$

Introducimos que la presión se anula en este caso:

$\dot{\rho}+3\dfrac{\dot{a}}{a}\rho=0$

Multiplicamos toda la expresión por 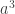$a^3$ :

$a^3\dot{\rho}+3a^2\dot{a}\rho=0$

Esto se puede escribir como:

$a^3\dfrac{d\rho}{dt}+3a^2\dfrac{da}{dt}\rho=0$

Si nos fijamos

$3a^2\dfrac{da}{dt}=\dfrac{da^3}{dt}$

donde hemos aplicado que

$\dfrac{d f^n(t)}{dt}=nf^{n-1}(t)\dfrac{df(t)}{dt}$ ,

entonces podemos escribir:

$a^3\dfrac{d\rho}{dt}+\dfrac{da^3}{dt}\rho=0$

Pero eso es la derivada de un producto:

$\dfrac{dfg}{dt}=f\dfrac{dg}{dt}+\dfrac{df}{dt}g$ ,

así que no es más que:

$\dfrac{d(\rho a^3)}{dt}=0$

Y dado que si la derivada de una función se anula indica que dicha función se anula, tenemos que:

$\rho a^3=C$

donde C es una constante, quedando que la densidad varía con el factor de escala como:

$\rho=\dfrac{C}{a^3}$

Si representamos la densidad $\rho$ (eje vertical) en función del factor de escala (eje horizontal) obtenemos una dependencia:

En esta gráfica hemos tomado C=1 por simplicidad.

Pero notemos que esto es lo que uno espera en este caso, lo que nos dice es que la densidad escala con el volumen. Es decir, si aumentamos el volumen al doble la densidad se reduce a la mitad y así sucesivamente. Es lo que tiene que pasar en una situación donde no hay producción de materia y donde no hay presión o flujos que puedan compensar la disminución en la densidad por el aumento del volumen.

La constante C

Hay que determinar el valor de esta constante. Esto se puede hacer de varias formas pero lo interesante es darnos cuenta de que la constante C que aparece ahí tiene que estar relacionado con un valor de la densidad, así que lo que podemos hacer es utilizar el valor de la densidad en el tiempo presente: 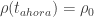$\rho(t_{ahora})=\rho_0$ es decir, el valor que ahora medidos en la densidad de materia del universo. Todas las cantidades con un subíndice 0 indicarán valores actuales:

$\rho=\dfrac{\rho_0}{a^3}$

Volveremos a esto más tarde y diremos cómo calcular ese valor de densidad actual.

Resolviendo la ecuación de Friendmann

Una vez que sabemos cómo se comporta la densidad en función del factor de escala estamos en disposición de resolver la ecuación de Friedmann para saber como se comporta el factor de escala en el tiempo.

Para mantener la discusión simple en esta entrada y en las siguientes consideraremos que en dicha ecuación la curvatura es nula, es decir, k=0.

Le dedicaremos un buen paquete de entradas a discutir la importancia de este factor y su influencia en los modelos cosmológicos.

La ecuación de Friedmann que hemos tratado hasta el momento es:

$\left(\dfrac{\dot{a}}{a}\right)^2=\dfrac{8\pi G}{3}\rho-\dfrac{kc^2}{a^2}$

Ahora nos centramos en el caso de curvatura nula:

$\left(\dfrac{\dot{a}}{a}\right)^2=\dfrac{8\pi G}{3}\rho$

Luego volveremos a discutir esto de la curvatura pero ahora el interés está en ver como se resuelven los casos sencillos de modelos cosmológicos.

Entonces vamos a resolver esta cuestión:

1.- Hemos determinado que la densidad depende del factor de escala como:

$\rho=\dfrac{\rho_0}{a^3}$

2.- Introducimos esto en la ecuación de Friedmann:

$\left(\dfrac{\dot{a}}{a}\right)^2=\dfrac{8\pi G}{3}\dfrac{\rho_0}{a^3}$

que se puede escribir, agrupando constantes, como:

$\left(\dfrac{\dot{a}}{a}\right)^2=\dfrac{8\pi G\rho_0}{3}\dfrac{1}{a^3}$

3.- Simplificamos un poco (eliminando algunos factores a que están a ambos lados de la ecuación):

$\dot{a}^2=\dfrac{8\pi G\rho_0}{3}\dfrac{1}{a}$

Esta es una ecuación diferencial que uno puede intentar (y se puede) resolver por los métodos tradicionales.

Pero los cosmólogos tienen otra forma más divertida de resolver esto, y es lo que ellos llaman por inspección.

El truco está en lo siguiente:

a) Sabemos que el factor de escala tiene que ser una función del tiempo. Pero seguramente será una función del tiempo elevado a alguna potencia $t^n$ .

b) Supongamos que 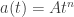$a(t)= At^n$ y veamos si eso puede satisfacer la ecuación. A, es una constante. Para ello hay que saber un par de cosas:

–> Cada derivada d/dt baja el exponente de n a (n-1).

–> Cada potencia del factor de escala a, por ejemplo 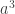$a^3$ , pues multiplica al exponente del tiempo por la misma cantidad, así que pasaría de n a 3n en el ejemplo.

Por lo tanto:

Lado izquierdo: El factor de escala aparece en: $(da/dt)^2$ Por lo tanto el exponente del tiempo quedaría (n-1) por la derivada, y luego 2(n-1) por la potencia.

Lado derecho: El factor de escala aparece como: 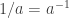$1/a=a^{-1}$ por lo tanto el exponente del tiempo quedaría multiplicado por -1. Así tendríamos un exponente -n.

Dichos exponentes tienen que ser iguales a ambos lados de la ecuación:

$2n-2=-n$

con lo cual tenemos 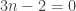$3n-2=0$ y la única solución sería: $n=2/3$ .

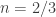Por lo tanto:

$a=At^{2/3}$

El valor de A

Para sacar el valor de A sólo hemos de pensar que lo que nos interesa es considerar que el factor de escala en el tiempo actual valga 1. Esto es así porque uno puede tomar ese valor como valor de referencia. Así que 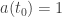$a(t_0)=1$ implica:

$a(t_0)=1=At_0^{2/3}$

Por lo tanto 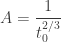$A=\dfrac{1}{t_0^{2/3}}$ . Entonces el factor de escala evoluciona como:

$a(t)=\left(\dfrac{t}{t_0}\right)^{\dfrac{2}{3}}$

Densidad, Factor de escala y Parámetro de Hubble

La densidad será:

$\rho(t)=\dfrac{\rho_0}{a^3}=\dfrac{\rho_0 t_0^2}{t^2}$

Cuya gráfica (densidad–eje vertical) vs (tiempo — eje horizontal) es:

Como vemos la densidad decrece con el tiempo, lo que ya esperábamos. (hemos puesto la constante =1 aquí sólo nos interesa el perfil de la gráfica para ver el comportamiento con el tiempo)

El factor de escala:

$a(t)=\left(\dfrac{t}{t_0}\right)^{\dfrac{2}{3}}$

Y graficando factor de escala vs tiempo: