Empezamos por lo más sencillo, explicar que es una cuerda dentro de esta teoría.
Bien, en realidad es la cosa mas sencilla del mundo, una cuerda (bosónica), matemáticamente, es una curva (real) que evoluciona en el tiempo.
¿Por que alguien se preocupó de trabajar en una cuerda cómo un objeto fundamental en vez de hacerlo con partículas puntuales?
La respuesta, curiosamente, es “nadie”.
La primera motivación para ocuparse de una teoría de cuerdas proviene de la cromodinámica cuántica, o más bien al estatus de la física de hadrones antes de aparecer la cromodinámica cuántica.
Sin entrar en muchos detalles señalar que se sabe que el neutrón y el protón, las partículas que forman el núcleo atómico no son partículas elementales, estan formadas por (3) quarks.
Esos quarks se describen por una teoría gauge, la SU(3).
Lo curioso es que si los quarks, y las partículas que median su interacción, los gluones, deben formar estados ligados (protones, neutrones, y en realidad todas las partículas hadrónicas) debe haber algo que impida que haya quarks libres, que nunca se han observado.
Eso llevó a que en un momento dado se propusiera un modelo fenomenológico bastante descriptivo. Los quarks estaban unidos por algún tipo de cuerda,
es decir, existían cuerdas que tenían un quark en cada uno de sus extremos,
el confinamiento (ausencia de quarks libres) se debería a que si se estiraba demasiado esa cuerda se rompía en dos nuevas cuerdas cada una con su pareja de quarks, en realidad un quark y un antiquark, en sus extremos (para el protón o neutron era necesario tres cuerdas unidas por un extremo entre sí y con un quark en los otros extremos).
Hacía falta ponerle mates a esa idea, y es lo que se hizo allá por el 75.
El problema es que esa teoria tenía un “inconveniente”, en su espectro aparecía una partícula de spin 2 que claramente no encajaba en el modelo de quarks, más adelante se re-interpreta la teoría de cuerdas cómo una teoría fundamental y esa partícula de spin 2 pasa a ser el gravitón.
He hablado que en el espectro de una teoría de cuerdas hay partículas, bien, esto significa, hablando de manera simplificada, que las cuerdas vibran y que cada modo de vibración se identifica con algún tipo de partícula.
Según esto cada partícula conocida sería un modo de vibración de una cuerda. Como ese rango de partículas incluye los fermiones (por así decirlo las partículas que forman la “materia”) y los bosones (las partículas que median las interacciones entre la materia) tenemos que la teoría de cuerdas sería una teoría que explicaría toda la física conocida, sería una teoría unificada.
Y además sólo tiene un parámetro libre, la tensión de la cuerda, así pués con la media de un sólo parámetro se tendría el valor de todos los demás parámetros de la física pues sería deducibles matemáticamente a partir de esa tensión.
Tras este previo sobre fenomenológia, no especialmente riguroso, vamos con algo de mates.
En matemáticas, geometría diferencial básica (sin usar formalismo de variedades), una curva es un lugar del espacio de dimensión uno que puede, en un sistema de coordenadas, describirse mediante una caracterización.
Aquí σ es el parámetro que describe la curva y las Xμ son las coordenadas.
El índice μ varia desde 0 hasta D-1, dónde D es la dimensión del espacio-tiempo donde se sitúa la cuerda.
Bien, esto es una curva, una cuerda es una curva que se deja evolucionar en el tiempo, es decir, que aparte de la dependencia en σ hará una dependencia en τ (tiempo propio).
Bien, esto es la “cinemática” de la cuerda, nada particularmente complicado, pasemos a la dinámica.
Cómo se ha discutido por aquí, y es bien sabido, en física la dinámica suele inferirse a través de una función lagrangiana, ¿que lagrangiana debe describir la cuerda? Bien, hay dos posibles, la más sencilla, conocida cómo la de Nambu-Goto surge de generalizar el lagrangiano de una partícula libre en relatividad especial, que recordemos es:
dónde, cómo es habitual en física, el punto sobre la coordenada denota derivación respecto al tiempo.
Esta acción representa la longitud de la línea de universo de la partícula relativista, es decir, una partícula puntual, matemáticamente un punto, al evolucionar en el espacio-tiempo describe una trayectoria, parametrizada por el tiempo τ.
La acción es la longitud (en la métrica de Minkowsky) de esa curva.
Pues bien, una partícula al evolucionar en el tiempo describe una curva
. Una curva al evolucionar en el tiempo describe una superficie, ergo la acción de Nambu-Goto de la cuerda va a ser el área (minkowskiana) de esa superficie:
Bien, esta acción es sencilla de entender, mera generalización de la acción de la partícula clásica. El problema es que aparece una raíz cuadrada, y eso, cuando se quiere proceder a tareas de cuantización, es algo muy molesto.
Así pues se prefiere usar otra acción, la de Polyakov.
El truco es expresar el área mediante una métrica intrínseca de la superficie, denotada por h, en concreto tenemos:
dónde la forma concreta para h es:
Bien, esta es la forma de la acción. En mecánica clásica una vez que tenemos la acción normalmente lo siguiente que hacemos es calcular las ecuaciones de movimiento asociadas a ella (ecuaciones de Euler-Lagrange).
Pero antes de hacer eso hace falta señalar unos aspectos importantes.
Esta acción, cómo muchas otras que aparecen en teoría cuántica de campos, tiene simetrías, es decir, existe un grupo de transformaciones de los campos que dejan invariante la acción. La acción de Polyakov tiene tres simetrías:
(i) Invariancia Poincaré , (ii) invariancia bajo difeomorfismos de la Worldsheet , y (iii)invariancia Weyl (invariancia de escala).
Estas invarianzas se expresan matemáticamente en términos del tensor energía-momento, análogo al de la relatividad general, cuya expresión es:
La invarianza bajo difeomorfismos implica que este tensor (que nos da cuenta de la energía y el momento de la cuerda) debe conservarse, es decir:
La invarianza Weyl se traduce en:  .
.
Bien, esto concluye la breve por ahora el análisis de las simetrías, vamos a poner la ecuación de movimiento:
* 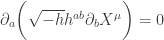
Una vez se tiene la ecuación de movimiento se debe proceder a resolverla.
Habíamos dicho que teníamos simetrías.
La invariancia de la acción bajo esas simetría se traduce en que hay grupos de soluciones equivalentes.
Necesitamos un modo de deshacernos de las soluciones redundantes, eso esta relacionado con las ligaduras de las que hablé en los post de LQG.
No obstante sin necesidad de saber los detalles de la teoría de ligaduras de dirac podemos entender bastantes cosas, sigamos.
Cuando queremos resolver ecuaciones diferenciales (en este caso en derivadas parciales) se imponen condiciones de contorno.
En este caso estas condiciones tiene interpretación cómo condiciones en los extremos de las cuerdas, tenemos cuerdas abiertas  (condiciones de Neuman) y cerradas
(condiciones de Neuman) y cerradas
En realidad más adelante se comprobó que había mas detalles a tener en cuenta en esto en relación con la teoría de branas, pero no merece la pena ocuparse de ello en esta introducción.
Tenemos las condiciones de contorno, vamos a proceder a encontrar soluciones a la ecuación de movimiento (*).
Para hacerlo hay primero que fijar un gauge, elegimos el conocido como gague conforme  ahí la ecuación de movimiento se reduce a la ecuación de Laplace y la solución nos queda para la cuerda cerrada:
ahí la ecuación de movimiento se reduce a la ecuación de Laplace y la solución nos queda para la cuerda cerrada:
y para la cuerda abierta:
dónde  son la posición y el momento del centro de masas de la cuerda.
son la posición y el momento del centro de masas de la cuerda.
Bien, hasta aquí lo básico, la parte clásica.
En la cuantización, que no trataré en este post, los α de las dos últimas ecuaciones se convertirán en operadores de creación/aniquilación que se corresponderían con las partículas observadas en la física del modelo standard.
Habrá que imponer la anulación de la derivada del tensor de energía momento lo quedará lugar a la famosa álgebra de Virasoro.
Y además habrá que comprobar que las simetrías de la teoría clásica se respetan, esto no es algo precisamente trivial, todo lo contrario, esas simetrías sólo se respetan si la dimensión (conocida como dimensión crítica) en que se propaga la cuerdas es distinta de 4.
Aquí he estado explicando la cuerda mas sencilla posible, la cuerda bosónica; para esta cuerda la dimensión crítica es 26 (25+1).
En realidad la cuerda bosónica no es realista, para empezar, cómo su nombre indica, no tiene nada mas que bosones en su espectro.
Cuerdas realistas requieren fermiones, eso implica introducir supersimetría y así entramos en el reino de las supercuerdas, par estas la dimensión crítica es 10 (9+1).
Desde luego hay muchísimo más que decir sobre la teoría de cuerdas, no en vano un libro de 750 páginas tiene algunos capítulos que más que un libro de texto parece un rápido review de resultados, pero creo que lo expuesto puede servir de orientación de a que nos estamos enfrentando al hablar de teoría de cuerdas.