lunes, 19 de octubre de 2015

Teorías de Kaluza-Klein ...

Voy a exponer cómo la teoría clásica del electromagnetismo, y otras teoría gauge, puede surgir de las dimensiones adicionales.

 Es lo que se conoce como el modelo de Kaluza, publicado allá por el 1919, con la RG recién salidita del horno.

Antes de ello hablar un poco del electromagnetismo en si mismo. La idea es sencilla, existen en la naturaleza unos campos E y B (eléctrico y magnético respectivamente) que afectan a unos cuerpos que tiene la característica de estar cargados eléctricamente.


El campo eléctrico y magnético se describen por las ecuaciones de Maxwell

\vec{ \nabla } \cdot \vec{E} = \rho \\
\vec{ \nabla } \times \vec{E} = - \frac{\partial \vec{B}}{\partial t} \\
\vec{ \nabla } \cdot \vec{B} = 0 \\ .
\vec{ \nabla } \times \vec{B} = \vec{j} + \frac{\partial \vec{E}}{\partial t}


Dónde \rho  es la densidad de carga y j la densidad de corriente (la corriente está asociada a que la carga se desplaza).

Bien, estas ecuaciones implican a los campos. 

Pero esos campos pueden derivarse de unos potenciales.

 La idea sencilla es que la variación de esos campos en el espacio de un punto a otro es lo que genera que haya una fuerza. 

Esa variación de un punto a oro se traduce en la derivada, claro.

 Así pues podemos expresar B y E en términos, respectivamente, de un potencial (tri)vector A y un potencial escalar V. 

Con estos podemos formar un cuadripotencial vector A4=(-V,A3).
La expresión exacta de los E y B en términos de los A y V es:


\bf{B}=\nabla \times \bf{A}
\bf{E}=\frac{\partial{\bf{A}}}{\partial t}-\nabla V

Lo interesante es que esas ecuaciones que definen E y B en términos de A y V no cambian si modificamos :

\bf{A}+\nabla G
V-\frac{\partial G}{\partial t}

Dónde aquí G es una función arbitraria de x,y,z, t.

 Pues bien, es esta indeterminación de los capos en términos de los potenciales lo que se conoce cómo invariancia gauge. 

En el caso del electromagnetismo surgió de manera ad hoc. Venia incorporada al introducir el concepto de potenciales.

 En otro post veremos cómo se puede relacionar esa invariancia con una invariancia bajo fases locales de una función de onda cuántica.

Lo primero es introducir el concepto de compactificar una dimensión. 

El primero en hacer esto fué Oscar Klein (no confundir con el célebre matemático Felix Klein). 

Si tenemos un campo escalar V \Phi (x,y) V dónde x representa el espaciotiempo normal e y una dimensión adicional de tipo espacial requerimos:

\Phi (x,y)= \Phi(x,y + 2\pi)

De esto se sigue que podemos expandir \Phi  en serie de Fourier

\Phi(x,y)= \sum_{n=-\infty }^{n= \infty } \Phi_n(x)e^{iny/r}

A consecuencia de la teoría cuántica, en un estado con un n dado la componente y del momento debe ser O(|n|\hbar/r) . 

Así para un radio lo suficientemente pequeño, r, sólo el estado n=0 aparecerá en el mundo de la física de “bajas energías” (i.e. E\ll\hbar c/r ).

En su versión moderna las teorías de Kaluza-Klein se materializan en las dimensiones extra de las teorías de cuerdas.

 En las primeras versiones, previas a la “segunda string revolution”,
 se consideraba que el radio de compactificación debía de ser del orden de la longitud de Planck, es decir:

r \approx l_P \equiv (\hbar G_N / c^3 )^{1/2} \approx 1.6 \times 10^{-35} m

De ese modo la masa de los estados excitados ( n \not= 0)  serían del orden de la masa de Planck M_P \approx 10^{19} GeV/c^2 , lo cuál sería imposible de obtener con los colisionadores actuales, o los fabricarles en un futuro cercano.

 En la segunda “string revolution” se introdujeron objetos cómo las D-branas, se comprobaron dualidades entre diversas teorias de cuerdas, surgió la teoría M, etc.

 Algunos de esas ideas llevaron a que la gente considerase la posibilidad de que alguna, o algunas, de las dimensiones extra del espacio-tiempo pudiera tener una dimensión mesoscópica (a medio camino entre lo macroscópico, digamos algo submilimétrico, y la longitud de Planck). 

En ese caso, entre otras cosas, los modos de Kaluza-Kklein de algunas partículas  podrían tener masas similares a las alcanzables en el LHC.

 Hasta ahora no se ha observado ningún signo de esos modos en las colisiones efectuadas a 8 TeV, así que hay límites severos para el tamaño de esas dimensiones mesoscópicas.

El modelo de Kaluza parte de considerar un espacio de 4 dimensiones espaciales y una temporal y compactificar en un círculo una de las espaciales. 

Denoto con M, N índices en 5 dimensiones y con \nu \mu  en 4.

Tenemos por tanto una métrica en 5 dimensiones g_{MN}  que vista desde 4 dimensiones se descompone del siguiente modo:

1. g_{\nu\mu}  La métrica habitual en 4 dimensiones.
2.g_{\nu4}=g_{4\nu}  Un campo vectorial en 4 d.
3.g_{44}  Un campo escalar en 4 d.

Denotamos x4 cómo y. Kaluza impuso la siguiente condición:

4.\frac{\partial g_{MN}}{\partial y}=0

¿Por qué? Bien, esto simplemente implica que los campos no dependen de la coordenada y. 

Por supuesto la coordenada y esta compactificada a un círculo, es decir se identifican los puntos y  e y +2.pi.r .

Cómo puede sospecharse fácilmente adónde queremos llegar es a que se puede identificar el campo vectorial de la ecuación 1 con el cuadripotencial del campo electromagnético A_\nu .

Para que la idea funciones se expande la métrica en términos de una serie de Fourier en la coordenada y:

5.g_{MN}(x,y)=\sum_n g_{MN}^n(x) .e^{iny/r}

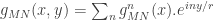
Ahora lo que se hace es una parametrización de la métrica, digamos una descomposición en la que queda:

6. g_{44}=k. \Phi
7.g_{4\nu}=k.\Phi.A_\nu  (y el antisimétrico)
8. g_{MN}=k.g_{\nu\mu} + \Phi.A_\nu

y dónde k=\Phi^{-1/3}

Escrito en forma matricial esto es

g_{MN}^{(0)} = \phi^{-1/3} \left( \begin{array}{cc} g_{\nu\mu} + \phi.A_\nu & \phi A_{\nu} \\ \phi A_{\nu} & \phi \end{array} \right)

Bien, esta es la métrica, pero la métrica es sólo parte de la historia. Lo que nos da la dinámica es la acción. 

Partimos de la acción para la ecuación de Einstein en 5 d que básicamente, y salvo factorcillos, es la integral de el escalar de Ricci asociado a esa métrica.
Lo interesante es que en las ecuaciones 6,7, 8 hemos descompuesto la métrica 5 d en términos de cantidades 4d.

Si calculamos el escalar de Ricci manteniendo explícitamente la presencia de esos campos 4 d obtenemos que la acción queda de la forma:

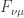S=-(2\pi.r)\int d^4xe/2G^2_5\left[ R + 1/4 \phi F_{\nu\mu}F^{\nu\mu} + 1/6\phi^2\partial^\nu\phi\partial_\nu\phi \right]

Dónde F_{\nu\mu}  es cómo podría esperarse el tensor campo electromagnético asociado al cuadrivector A_\nu  Y G es la constante gravitatoria en 5 dimensiones.

Así pues la invariancia bajo GCT (general coordinates transformations) de la gravedad en 5 dimensiones se traduce en que cuando una coordenada se compactifica en la aparición de un campo que cumples las mismas ecuaciones que el campo electromagnético y que por tanto tiene una invariancia gague local. 

Es decir, una invariancia interna aparece en este formalismo como una consecuencia de una invariancia externa al compactificar.

No he puesto todos los detalles, que llevaría mucho tiempo, pero espero que con esto se coja bien la idea.

De todos modos esta idea es sólo una pequeña parte del asunto de la compactificación. 

Nos hemos ocupado solamente de qué pasa cuando la métrica se compactifica, pero ¿qué pasa cuando se copactifica un campo cúantico fermionico sin masa?

 Más interesante aún ¿qué pasa si se compactifica un campo que ya en 5 dimensiones es un campo gauge?
Publicado por en