Paul Maurice Dirac
Vamos a comenzar con el estudio de los espinores. Como veremos estos son unos objetos matemáticos muy interesantes que aparecen en muchos rincones de la física. Por ejemplo, son esenciales para la descripción de los fermiones que son aquellas partículas de espín semientero y que son las que conforman la materia ordinaria en su nivel más fundamental. Ejemplos de fermiones son los electrones, los protones, los quarks, etc.
Antes de introducirnos en las peculiaridades matemáticas de los espinores tenemos que detenernos a estudiar la famosa ecuación de Dirac. Esta es una ecuación que combina la cuántica y la relatividad especial, es decir, describe el comportamiento cuántico de sistemas que se mueven de forma relativista.
Sin lugar a dudas, la ecuación de Dirac es una de las construcciones teóricas más importantes del siglo XX y cambió para siempre la forma en la que entendíamos la materia. Entre las maravillas escondidas en los trazos de esta ecuación podemos encontrar la explicación de la antimateria, la explicación y origen del espín de las partículas elementales y, quizás de una manera exagerada, toda la química.
Si buscamos en la literatura especializada podemos encontrar muchas derivaciones de esta ecuación. Lo maravilloso es que nació de la mente de Dirac en respuesta a los problemas que presentaba una descripción relativista de los fenómenos cuánticos. En esta entrada sobre la ecuación quiero proponer una forma de derivar la ecuación, puede que no sea la mejor, ni la más elegante desde el punto de vista matemático, pero es la que más me ha convencido para exponerla en el blog.
Relatividad, cuántica y sus problemas
Desde el mismo origen de la teoría cuántica se planteó el problema de describir sistemas cuánticos que se movieran a velocidades cercanas a la de la luz. Para conseguir esto se tenían que fundir los principios cuánticos y relativistas de forma que la descripción fuera consistente y libre de contradicciones internas.
El propio Schrödinger en su intento de fundamentar la idea de De Broglie, comenzó a postular una ecuación relativista, sin embargo rechazó la idea ya que planteaba graves problemas que no supo interpretar. La ecuación que Schrödinger descartó no era otra que la ecuación de Klein-Gordon.
Resumiendo, cuando intentamos describir una única partícula relativista en términos cuánticos lo que encontramos es que la ecuación nos da soluciones con energías negativas y lo que es peor, aparecen probabilidades negativas, por ejemplo a la hora de localizar la partícula.
Estos problemas son, a simple vista, devastadores. No tiene sentido hablar de energías negativas y mucho menos de probabilidades negativas. Sin embargo, pronto se vio que las energías negativas no eran un problema grave sino una virtud de la teoría que una vez reinterpretada la misma en términos de campos y no de partículas individuales da lugar a, entre otras cosas, la antimateria.
Lo de las probabilidades negativas fue un duro golpe para la teoría y muchos físicos se plantearon solucionar el problema. Entre ellos estaba Paul Dirac, y su forma de enfrentarse al problema nos regaló toda una nueva física.
Las exigencia relativistas
Observemos la ecuación de Schrödinger:
Es evidente que esta ecuación no puede ser relativista por simple inspección. ¿Por qué? Porque la ecuación involucra derivadas espaciales de segundo orden y la derivada respecto al tiempo es de primer orden. Para la relatividad el espacio y el tiempo tienen la misma categoría, así pues para que las expresiones matemáticas sean consistentes con la relatividad especial (entre otras muchas cosas) tenemos que exigir que las coordenadas espaciales y temporales tengan el mismo estatus.
La ecuación de Klein-Gordon solventa este punto proponiendo una ecuación, que no es más que escribir en términos de operadores la relación entre la energía y el momento relativista, que contienen derivadas segundas tanto respecto al tiempo como al espacio.
Sin embargo, como hemos comentado, esta ecuación da lugar a probabilidades negativas. El origen de estas probabilidades se puede rastrear hasta la derivada segunda del tiempo. Por lo tanto, Dirac se planteó el reto de conseguir escribir una ecuación que fuera consistente con las reglas de la relatividad especial pero que solo tuviera derivadas de primer orden respecto de las coordenadas espaciales y temporales.
Ecuación de Dirac, una derivación
La idea es muy simple, vayamos por pasos, (en lo que sigue trabajaremos con unidades  ):
):
- La relación entre la energía y el momento relativista se ha de cumplir en cualquier caso:
.
- Hagamos las sustituciones usuales en cuántica para la energía y el momento:
y
. Recordemos que
y
. Por lo tanto nos queda:
- Esta no es más que la ecuación de Klein-Gordon.
- Ahora, recordando que la ecuación de Schrödinger se puede escribir formalmente como:
. En este caso vamos a considerar que la parte de Hamiltoniano en la ecuación de Klein-Gordon en realidad es el cuadrado de un Hamiltoniano previo que podemos escribir con toda generalidad como:
- De forma que
.
y
son, en principio, cuatro constantes por determinar.
Desarrollemos pues el cuadrado de ese Hamiltoniano propuesto:
1.- 
2.- Escribiendo los sumatorios de manera explícita:
3.- Ahora, el primer sumatorio lo podemos separar en dos partes. La primera cuando i=j y el otro haciendo la suma para valores i>j simetrizando los productos para poder recorrer todos los términos requeridos para la suma. Los sumatorios que contienen productos  podemos renombrarlos para agruparlos:
podemos renombrarlos para agruparlos:
4.- Ahora imponemos que esto sea el Hamiltoniano de Klein-Gordon que es imponer la relación relativista entre la energía y el tiempo:
5.- En este punto podemos ir encontrando las relaciones que tienen que cumplir  y
y 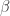 para que esto sea posible:
para que esto sea posible:
a)  (podríamos escribir 1, pero vamos a usar esta notación que adquirirá sentido en breve)
(podríamos escribir 1, pero vamos a usar esta notación que adquirirá sentido en breve)
b)  (podríamos escribir 1, pero vamos a usar esta notación que adquirirá sentido en breve)
(podríamos escribir 1, pero vamos a usar esta notación que adquirirá sentido en breve)
c)  para
para 
d) 
El anticonmutador
Podemos reescribir estas propiedades usando el anticonmutador. Dados dos objetos matemáticos, A y B, el anticonmutador { , }, calcula:
Si este objeto se anula, decimos que A y B anticonmutan y por lo tanto AB=-BA.
Así pues, tenemos:
a)  para
para  .
.
b) 
c)  para
para  .
.
Por lo tanto,  son objetos tales que su cuadrado nos da la unidad y anticonmutan entre ellas. Estas características hace que estos objetos no puedan ser número ordinarios, tienen que ser matrices.
son objetos tales que su cuadrado nos da la unidad y anticonmutan entre ellas. Estas características hace que estos objetos no puedan ser número ordinarios, tienen que ser matrices.
La ecuación de Dirac tiene la forma:
En esta aportación sería interesante entender y seguir los pasos que hemos dado para llegar a la ecuación de Dirac.
En la siguiente entrada nos centraremos en determinar quienes son esas matrices  y sus posibles realizaciones.
y sus posibles realizaciones.
Esas matrices serán la clave para llegar a las maravillas de la ecuación de Dirac.