sábado, 14 de noviembre de 2015

La importancia de la curvatura...

Vamos a tratar el tema de la curvatura.  Este término es muy importante, la cuestión es que en Relatividad General la geometría del espaciotiempo es parte del juego y en cosmología eso se ve en el hecho de que en la ecuación que rige la evolución del universo entra un término de curvatura:
La ecuación de Friedmann:   \left(\dfrac{\dot{a}}{a}\right)^2=\dfrac{8\pi G}{3}\rho-\dfrac{kc^2}{a^2}
donde el término 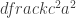dfrac{kc^2}{a^2} nos da la información de la curvatura del espacio (tres dimensiones) del universo.  Como veremos diferentes valores de 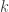k implican diferentes geometrías.  
Luego estudiaremos cómo afecta esto a la evolución del universo.

Los valores de 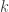k

La constante 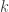k puede tener tres tipos de valores, positivo, negativo y nulo.  Cada caso está relacionado con una curvatura del espacio:
 Caso k=0
Este valor nos dice que el espacio es plano.  Es decir, las reglas de la geometría son las que aprendimos en el colegio:
– Dos rectas paralelas serán paralelas en todo momento.
–  Los tres ángulos de un triángulo suman 180º.
Caso 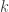k>0
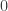
Si la constante es positiva implica que la geometría del espacio es “cerrada” (closed en inglés).  Es decir el espacio se asemeja a una esfera. A esto también se le llama geometría esférica:
–  No existen paralelas. Dadas dos líneas siempre acaban cortándose en un punto.
–  Los tres ángulos de un triángulo suman más de 180º.
Caso 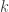k<0
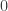
Si la constante es negativa implica que la geometría del espacio es “abierta” (open en inglés). Es decir, el espacio se asemeja a una silla de montar (en dos dimensiones). A esto se le llama geometría hiperbólica:
–  Existen infinitas paralelas.  Dada una línea podemos encontrar infinitas líneas que no se cortan con ella.
–  Los tres ángulos de un triángulo suman menos de 180º.
Uno siempre puede reasignar valores a la constante de forma que los tres casos correspondan a:  k=-1,0,1.

Influencia de la curvatura en la evolución del universo


En este apartado vamos a introducir una serie de razonamientos que son habituales en cosmología.  Lo que vamos a hacer es mostrar cualitativamente como influye la curvatura en la evolución del universo sin resolver explícitamente las ecuaciones.
Recordemos que tenemos las ecuaciones de Friedmann:
H^2(t)=\dfrac{8\pi G}{3}\rho-\dfrac{k}{a^2}
Para centrar ideas supongamos que estamos en un universo compuesto por materia (los argumentos funcionan igual en cualquier otro caso).  Recordemos, ver la entrada enlazada anteriormente, que en este tipo de universo la densidad se reduce al aumentar el factor de escala en una proporción 1/a^3.
Casos:
Constante positiva:
Si la constante es positiva la ecuación de Friedmann queda:
H^2(t)=\dfrac{8\pi G}{3}\rho-\dfrac{k}{a^2}
dado que hay dos términos restados es posible encontrar la situación en la que se compensen quedando entonces H(t)=0. 
 Pero recordemos que H(t) era:
H(t)=\dfrac{\dot{a}(t)}{a(t)}
es decir el ratio de la velocidad de expansión respecto al valor de la expansión en cada instante. 
 Si H(t)=0 significa que \dot{a}=0 por lo que la expansión se para.
Pensemos que la densidad \rho evoluciona como 1/a^3 y el término de curvatura (tomando k=+1) va como 1/a^2. 
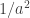Basta ir poniendo números cada vez más grandes para darnos cuenta de que en la competición:
\dfrac{1}{a^3}-\dfrac{1}{a^2}
llegará un momento en el que domine el término de la curvatura.  
Para eso hay que pasar por un momento donde H(t)=0, la expansión se para y después de eso   la gravedad sigue atrayendo a la materia y el universo empieza un proceso de contracción llegando a concentrarlo todo en un punto (esto sólo es cierto en un contexto clásico donde no entramos en detalles cuánticos ni en cambios de fases de la materia, notemos que aquí estamos considerando únicamente materia usual, lo cual no es lo que uno espera tener en el universo en todos los instantes. 
Ni mucho menos en los instantes iniciales o finales del mismo).
  Acabamos con un universo cerrado.
Constante de curvatura negativa
En este caso la ecuación de Friedmann queda (haciendo explícito el signo de k):
H^2(t)=\dfrac{8\pi G}{3}\rho-\dfrac{(-k)}{a^2}
Lo que podemos escribir como:
H^2(t)=\dfrac{8\pi G}{3}\rho+\dfrac{k}{a^2}
Es decir, tenemos dos términos que suman, cada vez es mayor por tanto H(t), lo que implica que la expansión es cada vez más rápida, el universo no para de expandirse y además lo hará aceleradamente.  
A esto lo llamamos universo abierto.
Constante de curvatura nula
En este caso la ecuación de Friedmann queda:
H^2(t)=\dfrac{8\pi G}{3}\rho
  Aquí tenemos que el universo se expandirá para siempre pero cada vez a un ritmo menor, idealmente el universo dejaría de expandirse (la velocidad de expansión se anularía) en un tiempo infinito.
Los tres comportamientos del factor de escala en función del tiempo dependiendo de los valores de k es:
Nos seguimos leyendo…
Publicado por en