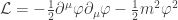Tal vez al lector que no sepa, o no tenga reciente, el tema de los lagrangianos,.
Aclaro, para evitar posibles confesiones, que en esta entrada me limito a la parte clásica y no a la formulación de integrales de camino de la mecánica cuántica y la QFT.
Empiezo por explicar cómo obtenemos un lagrangiano en mecánica clásica no relativista para objetos continuos, cómo puede ser una cuerda.
Aproximamos la cuerda por un conjunto de partículas en la posición xi unidas entre sí por un muelle, con lo cuál la energía potencial entre ellos sería un potencial de oscilador armónico sobre la diferencia de distancias.

1.
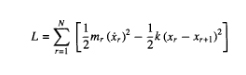
Si asumimos que la separación entre dos posiciones consecutivas es  y hacemos
y hacemos  nos queda el lagrangiano:
nos queda el lagrangiano:
2.
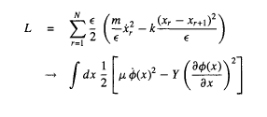
dónde hemos tomado los límites:
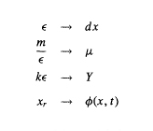
y dónde  es el desplazamiento de la partícula en x en el instante t.
es el desplazamiento de la partícula en x en el instante t.
Si usamos las ecuaciones de Euler-Lagrange para el lagrangiano de partículas , primera parte de la ecuación 2, y tomamos los límites correspondientes llegamos a la ecuación de ondas para la cuerda:
3.
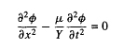
Aparte de partiendo de la primera parte de la ecuación 2 y tomando límites podemos llegar a la ecuación de otro modo.
Podemos partir de la segunda parte, el lagrangiano en el campo  , hacer una variación de ese campo y encontrar el valor del capo que minimiza esa variación. Enseguida vamos con los detalles porque éste punto de vista es el que nos interesa para el caso general.
, hacer una variación de ese campo y encontrar el valor del capo que minimiza esa variación. Enseguida vamos con los detalles porque éste punto de vista es el que nos interesa para el caso general.
Ahí partiremos de un lagrangiano, en general relativista, que dependerá no sólo de un campo sino también, opcionalmente, de sus derivadas.
4. 
dónde
5. 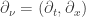
En general el lagrangiano de campos será la integral espacial de una densidad lagrangiana y la acción la integral en el tiempo de esa densidad:
6.
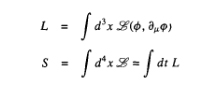
La variación de la lagrangiana viene dada por la expresión:
7.
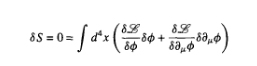
Si integramos por partes y revertimos la acción de la derivada llegamos a:
8.
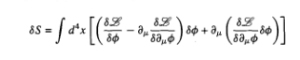
Cómo, de manera análoga al caso de la partícula puntual, el último término (llamado de frontera) se anula en los extremos de la integración llegamos a las ecuaciones de Euler-Lagrange para campos.
9.
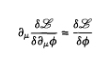
El caso mas simple, y que enlaza con la anterior entrada, es el lagrangiano de Klein-Gordon.
10.