
Saber si un algoritmo se detiene tras un número finito de pasos, el problema de la parada, es un problema indecidible. Alan Turing demostró en 1936 que no hay ningún algoritmo universal capaz de decidir si cualquier otro algoritmo parará o no aplicado a una entrada arbitraria. La idea de la demostración es similar a decidir si la frase “esta frase es falsa” es verdadera o es falsa (obviamente indecidible). ¿Existen problemas físicos que sean indecidibles? No sabemos si la Naturaleza es (o tiene que ser) computable (en el sentido de la tesis de Church–Turing). Luego la cuestión es imposible de resolver.
Se puede construir un algoritmo que simule un sistema físico, es decir, existe un sistema físico discreto, que incorpore en su formulación el problema de la parada de Turing. El resultado de dicha simulación física (o sistema físico discreto) será indecidible. Tras un alarde técnico el español David Pérez-García y dos colegas lo han publicado en Nature.
En concreto, demuestran que no es decidible si un sistema cuántico discreto con un hamiltoniano con invariancia ante traslaciones en el tiempo tiene un salto de energía (gap). Recuerda que el espectro de energía de un sistema cuántico puede ser continuo (tener un punto de acumulación) en el estado de mínima energía (sistema sin gap), o puede ser discreto con un salto finito entre los dos primeros niveles de energía (sistema con gap).
Este problema está relacionado con el problema del salto de masa en las ecuaciones de Yang-Mills puras (uno de los Problemas del Milenio del Instituto Clay de Matemáticaas, premiable con un millón de dólares [PDF]). Por supuesto, el nuevo artículo no implica que dicho problema no sea decidible (igual que el problema de la parada de Turing no implica que no haya infinitos algoritmos en los que podamos decidir si paran o no paran).
El artículo es Toby Cubitt, David Perez-Garcia, Michael M. Wolf, “Undecidability of the spectral gap,” Nature 528: 207–211 (10 Dec 2015), doi: 10.1038/nature16059, short version [8 pp.], arXiv:1502.04135 [quant-ph], full version [146 pp.], arXiv:1502.04573[quant-ph]. Más información divulgativa en Davide Castelvecchi, “Paradox at the heart of mathematics makes physics problem unanswerable,” News, Nature, 09 Dec 2015; critica el enfoque de muchos medios Luboš Motl, “Physics problems cannot be undecidable,” The Reference Frame, 10 Dec 2015.

¿Qué es computable (o calculable)? Según la tesis de Church–Turing, cualquier cosa que se pueda formular mediante un algoritmo. ¿Todos los números reales son calculables? No, pues hay una cantidad infinita numerable de algoritmos y los números reales son un conjunto no numerable (“Vídeo de “Los números que no se pueden calcular (Homenaje a Turing)” en Naukas Bilbao 2012,” LCMF, 03 Oct 2012). Por tanto, con probabilidad uno, un número real elegido al azar no será computable. En Física usamos el concepto de número real para describir la Naturaleza, aunque solo podemos realizar operaciones con números computables. No pasa nada, pues la Física describe modelos de la realidad.
Más aún, las simulaciones físicas de la Naturaleza mediante ordenadores usan un número finito de números (los que se pueden representar en aritmética flotante en el ordenador) y nadie duda de que sean simulaciones realistas útiles en ingeniería.
¿Qué es un algoritmo? La tesis de Church–Turing afirma que el concepto de algoritmo es equivalente a una máquina de Turing; hay muchos otros modelos matemáticos del concepto de algoritmo, pero todos son matemáticamente equivalentes a una máquina de Turing y entre sí.
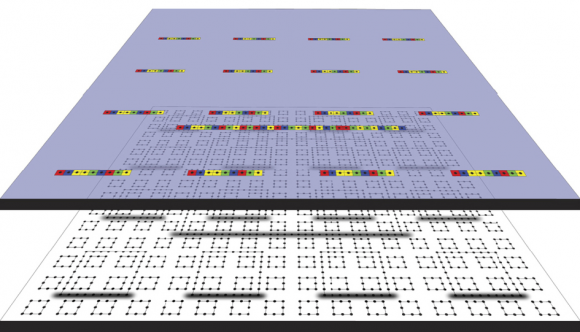
Si no sabes lo que es una máquina de Turing (la cinta de colores en la figura de arriba), porque no hayas estudiado informática, o porque no hayas leído el famoso libro de Roger Penrose “La nueva mente del emperador” (Oxford Univ. Press, 1989), lo siento, no te lo voy a explicar (consulta la wikipedia). Resumiendo hasta el extremo, una máquina de Turing (universal) es un modelo matemático del funcionamiento de un ordenador (en rigor, todos los ordenadores son máquinas de Turing).
Cubitt, Pérez-García y Wolf usan una máquina de Turing cuántica. La tesis de Church–Turing–Deutsch afirma que el concepto de algoritmo cuántico es equivalente a una máquina de Turing cuántica. Además, David Deutsch en 1985 demostró que toda máquina de Turing cuántica (o máquina de Deutsch) es equivalente a una máquina de Turing (clásica); no hay nada que una máquina cuántica pueda calcular que no pueda calcular una clásica, y viceversa (aunque Stuart Hameroff no lo sepa, porque no entiende a su colega Roger Penrose).
El problema de la parada de máquinas de Turing cuánticas es idéntico al problema de máquinas de Turing (clásicas).
Como puedes imaginar, para incorporar un algoritmo no decidible en la formulación matemática de un sistema físico cuántico (el sistema bidimensional de espines cuánticos con interacción entre vecinos que aparece en forma de grafo en la parte de abajo de la figura de arriba) conviene formular dicho algoritmo usando una máquina de Turing cuántica.
Pero ello no cambia nada el resultado, solo facilita la descripción matemática. Por cierto, si no sabes lo que es el espín y qué es un sistema de espines con interacción entre vecinos, lo siento, tampoco te lo voy a explicar (consulta la wikipedia).
El espectro de energía de un sistema cuántico es el conjunto de niveles de energía para sus posibles estados. Este espectro puede ser discreto, cada par de niveles de energía está separado entre sí por un salto (gap), o puede ser continuo, los niveles de energía corresponden a números reales, o puede ser una combinación de ambos (el espectro discreto presenta regiones con espectro continuo). Todo sistema cuántico estable tiene un estado fundamental, un nivel mínimo de energía.
El sistema tiene un salto de energía (gap) si el siguiente nivel de energía está separado del fundamental; pero hay sistemas sin salto de energía (gapless) en los que el nivel fundamental es el nivel de energía más bajo de un espectro continuo.
Cubitt, Pérez-García y Wolf estudian si es decidible el problema de determinar si un sistema cuántico concreto tiene gap o no tiene gap.
Para ello introducen un sistema cuántico en forma de red plana de espines cuya interacción entre vecinos depende de los resultados de la ejecución de una máquina de Turing cuántica. Para cualquier máquina de Turing se puede construir el sistema correspondiente. Por ejemplo, para la máquina de Turing universal que Turing usó en su demostración de que el problema de la parada no es decidible.
Repito, tras un sorprendente alarde técnico, la definición de su sistema cuántico garantiza que el espectro tendrá un salto de energía (gap) si dicha máquina de Turing para y no tendrá salto de energía (gapless) si dicha máquina de Turing no para. Por tanto, ¿se puede decidir si dicho sistema cuántico tiene gap o no lo tiene? No, porque el problema de la parada no es decidible.
En resumen, la conclusión general es que el problema de saber si un sistema cuántico discreto tiene o no tiene salto de energía no es decidible.
¿Significa esto que la Naturaleza no es decidible?
No, por supuesto que no. Dicho sistema cuántico se puede construir físicamente, igual que se puede implementar en tu ordenador la máquina de Turing universal que usó Turing en su demostración, pero ello no implica nada sobre la Naturaleza (o la Física) en general.
La tesis sobre la Naturaleza es computable o no es computable, o sobre si es decidible o no es decidible, no tiene nada que ver con el artículo que se acaba de publicar en Nature.
Y, repito para los despistados, ¿significa este nuevo teorema matemático que el problema del salto de masa para las ecuaciones de Yang–Mills no es decidible? No, por supuesto que no. Igual que el problema de la parada no implica que no existan algoritmos en los que podemos decidir si paran o no (la mayoría de los estudiados por los alumnos de informática durante su carrera).
Si te atreves (y quieres dedicar algunas décadas de tu vida a ello), aún puedes resolver el Problema del Milenio y ganar el correspondiente millón de euros.
No es fácil, pero intuyo que no es imposible.
No hay comentarios:
Publicar un comentario