Mecánica cuántica from a dummy. Que no te lo cuenten 2 - Cuentos Cuánticos

Retomemos el pico y la pala para seguir nuestro camino por la cuántica. Continuaremos por donde lo dejamos en la entrada anterior:

Mecánica cuántica from a dummy. Que no te lo cuenten 1

En esta primera entrega vimos como seleccionar estados y como definir operadores sobre los mismos.  

Hoy vamos a presentar dos conceptos, la superposición cuántica y los valores esperados de los observables con lo que trabajamos.

Esos estados propios

Nuestro ejemplo versa sobre un sistema cuántico que tiene una propiedad que hemos denominado color, representado matemáticamente por . 

Los estados propios, aquellos que no cambian más allá de verse multiplicados por un número al ser enfrentados a , son el estado blanco y el estado negro:

La importancia que tienen esos estados que son mutuamente excluyentes, o que son propios del observable que estemos trabajando, en este caso , es que son la base para construir todos los posibles estados del sistema.

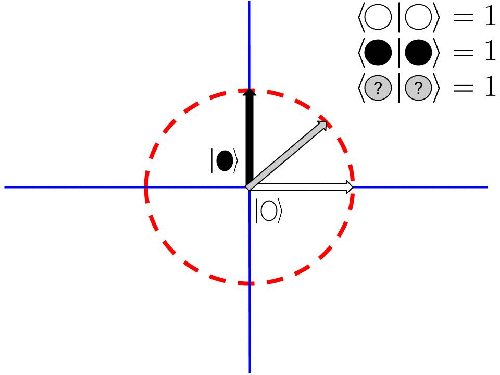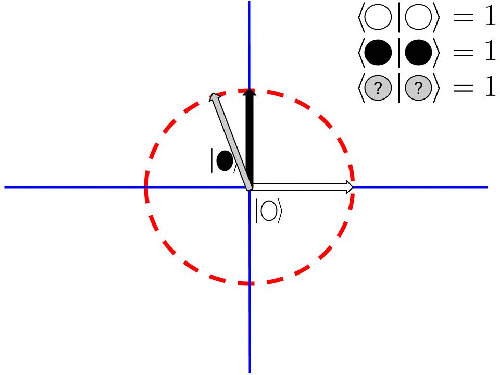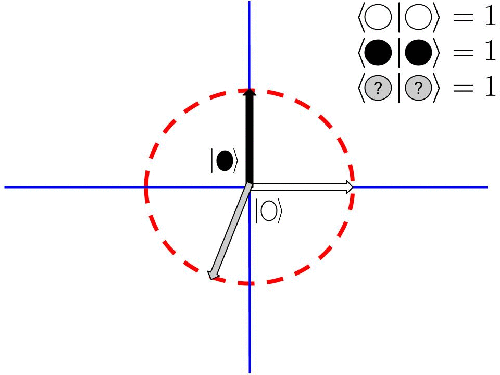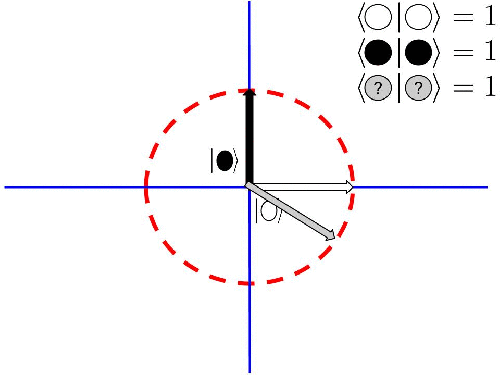
Haciendo un alarde de desmesura pongamos estos estados en unos ejes, como si fueran vectores:

Si ahora nos preguntamos, ¿cuáles son todos los posibles estados cuánticos admisibles?   La respuesta que nos da la mecánica cuántica es la siguiente:  Todas las combinaciones que podamos hacer de esos estados considerándolos como vectores.

Una combinación o superposición de estados no es más que sumar (o restar) esos estados multiplicados por coeficientes:

Los coeficientes ,  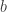pueden ser, en principio, cualquier número (de hecho, en general serán números complejos, pero no nos acomplejaremos por ello).

Considerando que nuestros estados se pueden entender como vectores, las dos primeras relaciones las interpretaremos como que los vectores blanco y negro tienen un módulo (longitud) al cuadrado que vale 1.  

Por lo tanto su longitud es la unidad. 

El segundo par de relaciones indican que los vectores blanco y negro son perpendiculares entre sí.

Retomemos un segundo nuestro estado superpuesto:

Para simplificar el asunto vamos a ponerle un nombre, para escribir menos y tal.  Yo he elegido este símbolo:

Para calcular el módulo al cuadrado de ese vector solo tendríamos que hacer lo siguiente:

Expresado en términos de la superposición queda:

Nota para los supercampeones:

 Si los coeficientes a y b son números complejos al darle la vuelta a los paréntesis esos de los estados hay que transformar los coeficientes en sus complejos conjugados.  Solo era eso.

En este punto hay que aplicar la propiedad orgiástica de la multiplicación, todos con todos, la propiedad distributiva creo que le dicen por ahí.

Eso parece un poco infumable, pero… ¡Nosotros sabemos los resultados de los productos de estados!  ¡Yuuuuuhuuuuu!

¡Fabuloso!, el módulo al cuadrado de la superposición lineal de estados no es más que la suma de los cuadrados de los coeficientes de la superposición.

Pero la cuántica tiene un capricho, la suma de los cuadrados de todos los coeficientes de una superposición ha de valer siempre 1. 

 Visto desde el punto de vista de vectores, resulta que las superposciones cuánticas están siempre contenidas en la circunferencia de radio 1 que definen los estados base, en nuestro caso el blanco y el negro:

Cualquier combinación de estados superpuestos cuyos coeficientes al cuadrado sumen 1 están sobre esa circunferencia. 

 Acabamos de identificar todos los estados posibles de este sistema respecto de esta característica que hemos llamado color.

La razón de este capricho, muy entre comillas, quedará clara en lo que sigue. Ahora ten fe y continúa el camino (seguro que esto te suena de algo, la diferencia es que aquí vamos a entenderlo todo).

No todos son propios

Al principio habíamos identificado los estados propios del operador que representa la magnitud color en nuestro sistema:

La pregunta es entonce si la superposición de estados propios de un observable (operador) sigue siendo un estado propio. 

 Más visualmente:

Es decir, ¿se queda el estado superpuesto exactamente igual salvo una multiplicación por un número al enfrentarlo al operador de color? 

 Veámoslo:

El operador  se enfrenta a cada término:

El operador , y todos los operadores cuánticos, no ve a los números,

 Estos operadores son transparentes para los números y solo se enfrentan a los estados cuánticos. 

Algo así:

Con lo que la historia queda:

Pero nosotros sí sabemos cómo actúa  sobre los estados blanco y negro ya que estos son propios de dicho operador.  

Con lo que tenemos:

Este resultado es bastante aleccionador, eso de ninguna de las maneras se puede escribir como la superposición original (que entre otras cosas tenía una suma en vez de una resta de estados).  

Por lo tanto, el estado que resulta de aplicar  a una superposición de estados propios del mismo no es, en general, un estado propio, no se puede escribir como el mismo estado multiplicado por un número como resultado final.

  Y esta es una lección muy importante.

Los valores esperados

A estas alturas de la película todos deberíamos de poder hacer los cálculos que se van a indicar aquí pero que no voy a desarrollar. 

 Como hemos visto, al hacer actuar un operador sobre un estado este cambia irremediablemente. 

 Bueno, no todos los estados sufren de ello, para cada operador se pueden encontrar un clase de estados que no cambian bajo su actuación, son sus estados propios (de los que hemos visto un ejemplo).

Pero bueno, esto es física, así que sería genial poder tener algo con que comparar los resultados teóricos y los resultados experimentales. 

 Para conseguir ese propósito, que veremos en todo su esplendor en sucesivas entradas, vamos a introducir el valor esperado del operador  en un determinado estado. 

 El valor esperado depende del estado con el que se calcule.  

Representaremos el valor esperado por .

Los valores esperados calculados con estados propios son simplemente los números que multiplican al estado tras la acción del operador correspondiente.  En nuestro caso por lo tanto tendríamos:

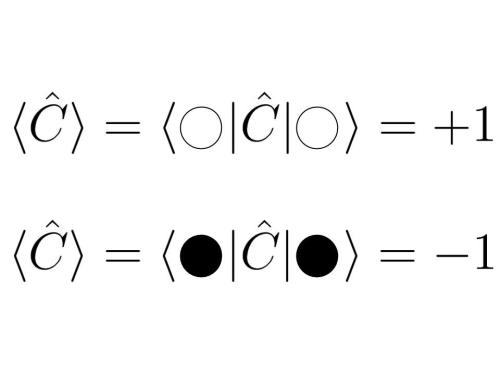
Desarrollemos, por cortesía porque seguro que no hace falta, uno de ellos, el valor esperado del color en el estado blanco.

¿Te atreves a calcularlo para el estado propio negro?

Ese es fácil, ¿qué tal este?

Es importante que calculemos ese valor esperado sobre el estado superpuesto. En la siguiente entrada vamos a explicar por qué hemos hecho todo esto y qué significan estas cosas pero antes de meternos en explicaciones con mucho movimiento de manos sería genial que nos hubiéramos enfangado en estos cálculos un rato.  

Verán como después de pelear con los simbolitos y haber llegado al resultado luego la explicación se entiende perfectamente, el motivo:

 La has amasado con las manos.

Cualquier cosa por aquí andaré.

Nos seguimos leyendo…