Caos espectral en mecánica cuántica...

Hace unas fechas escribí una breve reseña sobre caos cuántico. 

La ligereza de la misma puede haber servido cómo pista de que no era un tema en el que hubiese profundizado demasiado, por decirlo suavemente.

 El motivo es que no era un tema que me hubiese resultado especialmente atractivo hasta ahora. 

Cómo dije ahí esa gente tiente a ocuparse de mecánica cuántica muy sencilla y -además- en última instancia no existe un análogo cuántico del caos clásico así que no terminaba de ver un buen motivo para profundizar en ese campo.

Con los precedentes anteriores uno podría plantearse cómo es que ahora dedico una segunda entrada al tema. 

El motivo proviene de algo aparentemente muy alejado de la mecánica cuántica: el cálculo numérico.

 Cómo parte de la titulación de matemáticas es necesario cursar al menos dos asignaturas sobre cálculo numérico.

 En el primer año se ven varios temas relativamente sencillos cómo cálculo de ceros de funciones, interpolación de funciones, integración/derivación numérica, resolución de sistemas lineales y, la parte mas extensa, álgebra lineal numérica.

En los cursos de álgebra lineal se aprende a calcular autovalores y autovectores de manera analítica. 

Cómo suele ser habitual el método que es eficiente para hacer algo con “lápiz y papel” dista mucho de ser el mejor para hacerlo mediante algoritmos en un ordenador. 

En el caso del álgebra numérica sucede lo mismo, pero, además, se aprenden algunos hechos tan interesantes cómo sorprendentes.

Recordemos que para calcular los autovalores de una matriz M uno debe hacer el determinante de .

 Esto da cómo resultado un polinomio en .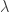

 Una vez se tienen las raíces de ese polinomio se sustituyen en la expresión  y se calculan el/los autovectores correspondientes a ese autovalor. 

En los ejercicios típicos las matrices están “cocinadas” para que el polinomio tenga raíces enteras (o al menos alguna de ellas entera y que el resto puedan obtenerse a partir de ahí por el método de Rufini).

 Por supuesto en problemas reales no sucede eso casi nunca (no estoy 100% seguro pero creo recordar que en el conjunto de todos los polinomios los que cumplen eso tendrían medida nula -definiendo una medida más o menos natural en el espacio de polinomios, claro-). 

Por ese motivo, en la práctica, uno debería resolver el polinomio por métodos numéricos y luego implementar un algoritmo que calculase el autovector a partir de ese autovalor.

El caso es que esa tarea tan sencilla de calcular las raíces de un polinomio tiene sutilezas inesperadas. 

La clave del asunto es que polinomios muy similares pueden tener raíces no tan similares. 

Es decir, una pequeña incertidumbre en el valor de un coeficiente del polinomio se traduce en una gran diferencia entre los valores de las raíces, osea, cómo exclamaría Malcom: ¡CAOS!. 

Antes de seguir con consideraciones teóricas sobre esto dejo un ejemplo de matriz cuyo polinomio característico tiene esa sensibilidad:

Uno puede hacer el polinomio característico y verificar que sus raíces son {1,2,3}. 

Si uno modifica muy ligeramente esa matriz, por ejemplo modificando el segundo elemento de la diagonal de 180 a 180.01 podría comprobar (recomiendo usar algún programa informático) que las nuevas raíces el polinomio característico (vamos, los autovalores de la matriz), son { 0.207, 2.3008, 3.50}

 Es decir, una modificación de uno de los elementos de la matriz del orden de  modifica todos los autovalores en magnitudes entorno al 50% lo cuál es algo realmente impresionante. 

En los libros o manuales elementales sobre cálculo numérico no se suele comentar mucho más al respecto y se pasa directamente a enseñar métodos para el cálculo de esos autovalores (según en que manuales se limita al método de potencias para el cálculo del autovalor dominante) y autovectores (normalmente el método QR y variantes)

 Tampoco suelen hacer las cuentas de cómo cambian los autovectores así que me hice el cálculo para los dos casos anteriores.

 Para la matriz original los autovectores también son bastante distintos, con variaciones incluso mayores que las de los autovalores.

El caso es que para alguien con una base de física una matriz es, sobre todo, un operador cuántico (para un matemático una matriz puede ser un montón de cosas, y dependiendo del caso se la estudia de muchas maneras diferentes xD), los autovalores las autoenergías (si el operador es el hamiltoniano) y los autovectores las autofunciones de onda cuánticas. 

Y claro, inmediatamente (al menos yo es lo que pensé nada mas leer ese resultado) es que si un operador cuántico tiene un comportamiento tan exótico uno podría pensar que algo extraño podría pasar con Mary…digo la cuántica ;). 

El caso es que no pude dedicarme inmediatamente a profundizar en ese hecho chocante, pero siempre estuvo ahí en segundo plano, cómo una inquietud, y en cuanto se dio la oportunidad analicé más a fondo el asunto.

 La primera duda que surge es sí esa incertidumbre en el cálculo de autovalores es debida a errores de redondeo en algoritmos numéricos o si obedece a una causa mas fundamental.

 En concreto plantean el caso del polinomio 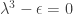 cuya solución  que no es derivable en el entorno de 0 y ese es el origen de la sensibilidad del polinomio.

 En un ejemplo mas complejo de una matriz, dependiente de un parámetro, que originaba polinomios “sensibles” a variaciones de ese parámetro.

 Esa matriz era además simétrica (autoadjunta) lo cuál es bueno pues los operadores cuánticos deben ser autoadjuntos. 

Con eso ya se tiene bastante información relevante, el problema es “fundamental” y no de redondeo, se identifica el problema (o al menos un factor del mismo) y se pueden analizar familias de matrices, no una sola.

La siguiente reflexión que a uno se le ocurre es plantearse cómo puede suceder esto con sistemas lineales.

 Al fin y al cabo la cuántica es lineal, y uno aprende, estudiando Sturn-Liouville (bien sea mediante análisis clásico o, de modo riguroso, en cálculo funcional) que la clase de operadores lineales autoadjuntos son buenos y maravillosos y nos dan una base del espacio de Hilbert de soluciones del problema ¿que más se puede pedir?.

 Bien, el caso es que bajo esa aparente inocencia los operadores lineales (incluidos los autoadjuntos) ocultan muchas sorpresas y uno, a poco que los estudie, se da cuenta de que son unos grandes desconocidos que guardan en su interior muchas pautas insospechadas. 

Pero, volviendo al principio, si la cuántica es lineal ¿de dónde surgen todas estas “sensibilidades”?

 Bien, los operadores son lineales, sí, pero las operaciones para extraer información de ellos (sus autovalores y autovectores en el caso de la cuántica) implican formar expresiones no lineales. 

La tarea de obtener el determinante es no lineal, y para calcular autovalores el resultado de la misma es un polinomio no lineal.

 Digamos que hay mucha no-linealidad escondida.

Bien, esa es la matemática, pero queda analizar un poco como afecta eso a la física.

 La idea básica -en un esquema meramente formal- es muy simple. 

Tenemos un sistema cuántico, todo lo particular que haga falta, cuyo hamiltoniano podemos considerar que es, en alguna base apropiada, una matriz finita.

 Los elementos de esa matriz en general van contener términos que se deben obtener de manera experimental (por ejemplo si es el hamiltoniano de un electrón en un campo eléctrico el valor de ese campo podría ser un dato experimental).

 Entonces eso significa que tenemos dos Hamiltonianos, H y H’ que difieren por una pequeña cantidad.

 Siguiendo la costumbre de teoría cuántica de perturbaciones podríamos escribir 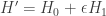 aunque, en este caso, no nos importa (necesariamente) que  sea resoluble analíticamente.

 La idea es que uno podría esperar que los autovalores de H y H’ fuesen muy similares (es el fundamento de la teoría de perturbaciones, en particular ahí se exige, cómo prueba de consistencia, que la diferencia entre un autovalor del sistema sin perturbar y el perturbado sea menor que la diferencia entre dos autovalores del sistema sin perturbar). 

Pero, cómo acabamos de ver, esto no siempre tiene porque suceder.

 Más adelante descubrí que hay una línea muy reciente de investigación, liderada por Michel Berry (el de la famosa fase de Berry) y llaman a esto “perturbación crítica”. Aún tengo que explorar mas el tema de lo que hace esa gente y cuanto se parece a lo que yo estoy considerando.

Pero sigamos con el quid de la cuestión. 

La idea es que dos sistemas con hamiltonianos muy similares pueden tener energías muy diferentes.

 Podría darse el caso medir el campo eléctrico del hamiltoniano con precisión de varios decimales y que pudiésemos resolver el problema y aún así los resultados no nos servirían para predecir, en la práctica los valores posibles de las energías.

 Pero puede ser peor aún, cómo los autovectores, que son las funciones de onda, también cambian mucho.

 Imaginemos que el campo eléctrico fluctúa en el tiempo.

 Si colocásemos el sistema en un estado inicial de superposición y midiéramos las frecuencias con las que se da cada autovalor de la energía estas no tendrían una distribución probababilística. 

El motivo es que al fluctuar el campo fluctuan los autovalores y no siempre estamos trabajando con autoenergías similares. Y, cómo además varían los autovalores, las probabilidades de ocupar cada autovalor también fluctúan. 

Es decir, podríamos tener un sistema del que sabemos el Hamiltoniano con mucha precisión, poder resolverlo analíticamente, y aún así, en la práctica, no poder obtener ninguna información útil respecto a que nos vamos a encontrar.

Para tratar esos sistemas- creo yo, habría que optar por una descripción en términos de ecuaciones diferenciales estocásticas (para una introducción ver por ejemplo este pdf) en la que aparte del término determinista (la ecuación de Schröedinger) habría un término de “ruido”. 

Eso sí, ese término no tendría porque ser browniano sino que su naturaleza dependería de la naturaleza analítica del parámetro del hamiltoniano que dicta la “sensibilidad” del mismo y podría bautizarse algo así cómo “ruido espectral”.

Para ir concluyendo hago una reflexión importante.

 Esto no es caos cuántico. 

En un sistema caótico clásico tenemos que la dinámica (el hamiltoniano) es fijo y hay sensibilidad en las condiciones iniciales (que no pueden medirse con precisión infinita).

 En cuántica el observable fundamental es la función de onda y no las posiciones/momentos. 

Y la unitariedad de la evolución cuántica implica que si las funciones de onda en un instante dado difieren por una cantidad pequeña esa diferencia se mantendrá constante en el tiempo. 

Esto plantea una duda conceptual de cómo si la realidad es cuántica en sistemas clásicos, que son el límite de los cuánticos (teorema de Erenfest) puede haber caos. 

Por supuesto mi argumento no implica que haya caos cuántico porque aquí lo que tenemos es algo distinto. 

Tenemos que el propio hamiltoniano (lo que dicta la dinámica) es el que está sujeto a una incertidumbre experimental y cómo consecuencia de la misma los observables cuánticos (autovalores, autofunciones) son muy sensibles a variaciones de esa incertidumbre. 

Por supuesto, y esto sería curioso de analizar en comparativas, en sistemas clásicos también hay esa incertidumbre en el valor exacto del hamiltoniano, y también hay operaciones de obtener autovalores y autovectores para obtener soluciones en algunos de esos sistemas (por ejemplo osciladores armónicos acoplados) así que esta sensibilidad extra, esta “perturbación crítica” afectaría por igual al mundo clásico y al cuántico, y tal vez (o tal vez no, vaya usted a saber xD) seria interesante comparar las diferencias entre ambos mundos para esos sistemas.

Para finalizar algunas palabras sobre lo que hace la gente de caos cuántico, que está relacionada con la naturaleza de los autovalores de los operadores audoadjuntos. 

Resulta, por ejemplo, que los hamiltonianos que presentan simetrías tienen una distribución de los autovalores muy diferente de los que no tienen simetrías (si se quieren buscar detalles usar los términos “quantum chaos, random matrix). 

Es un tema curioso, sobre el que tal vez lea mas, o tal vez no. 

Pero tras ver esto de la sensibilidad de los autovalores y que la distribución de los mismos depende de las simetrías del hamiltoniano está claro que bajo su inocente apariencia los operadores autoadjuntos tal vez puedan ocultar auténticos “animales patológicos” en su interior y que posiblemente la mecánica cuántica mas elemental guarde aún muchas sorpresas importantes en contradicción con la idea de que es un “animal doméstico y conocido”. Y eso si nos restringimos a cuántica elemental, y estudiando matrices finitas (a saber que pasa con las infinitas que son lo común en mecánica cuántica). 

Pero el caso es que las teorías cuánticas de campos también son, en el fondo, teorías cuánticas “normales” y, no sé ¿cómo podría ser el grupo de renormalización de un hamiltoniano de campos que fuera el análogo de uno de partículas “sensible”?

 ¿Tal vez el flujo de renormalización hiciese evolucionar el valor de las constantes de acoplo de manera caótica según nos movemos hacia energías mas altas? O, si la estructura de los autovalores depende de la simetría ¿que pasa en los fenómenos de ruptura espontánea de simetría?

En definitiva, que me da la impresión de que el formalismo de la mecánica cuántica convencional puede ser mucho, mucho mas rico de lo esperado, y que, por ejemplo, tal vez algunos fenómenos que por argumentos de “naturalidad” podrían parecer muy improbables a lo mejor no lo sean debido a que en algún punto hay alguna “sensibilidad” oculta en algún punto.